
今回は,縦軸が圧力$p$,横軸が体積$V$の$pV$図から,縦軸が絶対温度$T$,横軸が体積$V$の$TV$図の変換に関する問題を扱います.
入試でもときどきみかけますね.
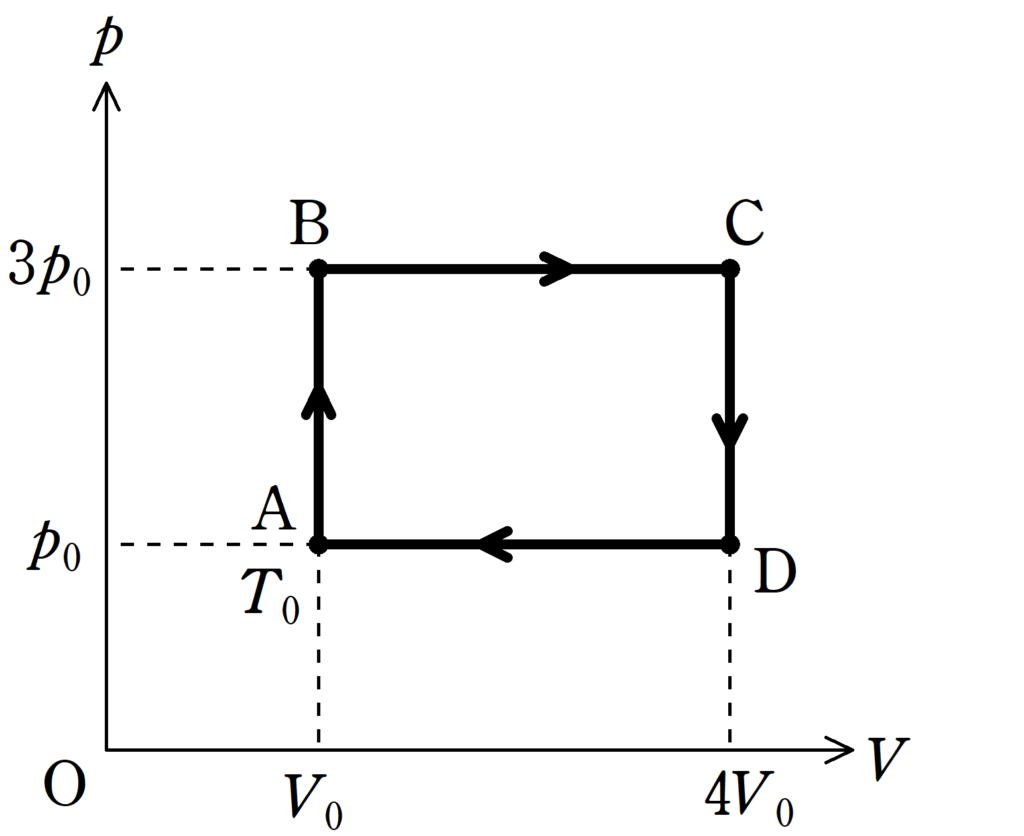
縦軸が理想気体の圧力$p$,横軸が体積$V$である,上図の$pV$図において,状態Aの圧力は$p_{0}$,体積は$V_{0}$,絶対温度は$T_{0}$であった.
また,状態B,C,Dの圧力はそれぞれ,$3p_{0}$,$3p_{0}$,$p_{0}$,体積はそれぞれ$V_{0}$,$4V_{0}$,$4V_{0}$である.
状態A→B→C→Dのように状態を変化させるとき,次の問いに答えよ.
(1) 状態B,C,Dの絶対温度$T_{\rm B}$,$T_{\rm C}$,$T_{\rm D}$を求めよ.
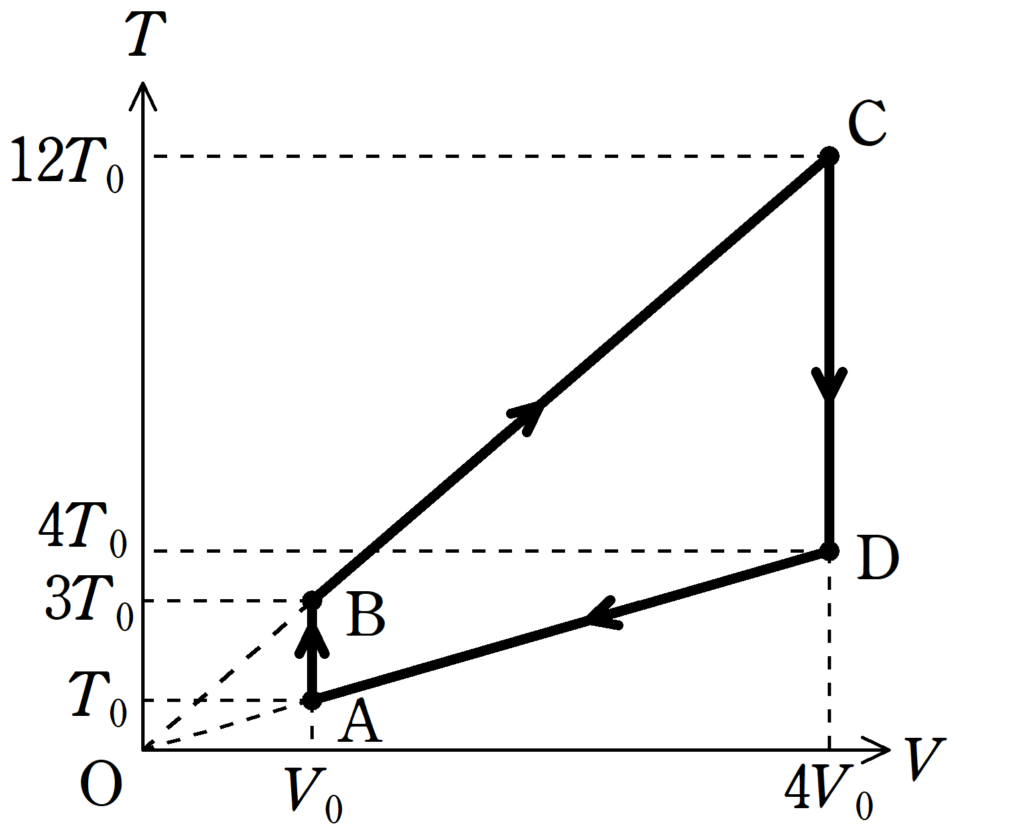
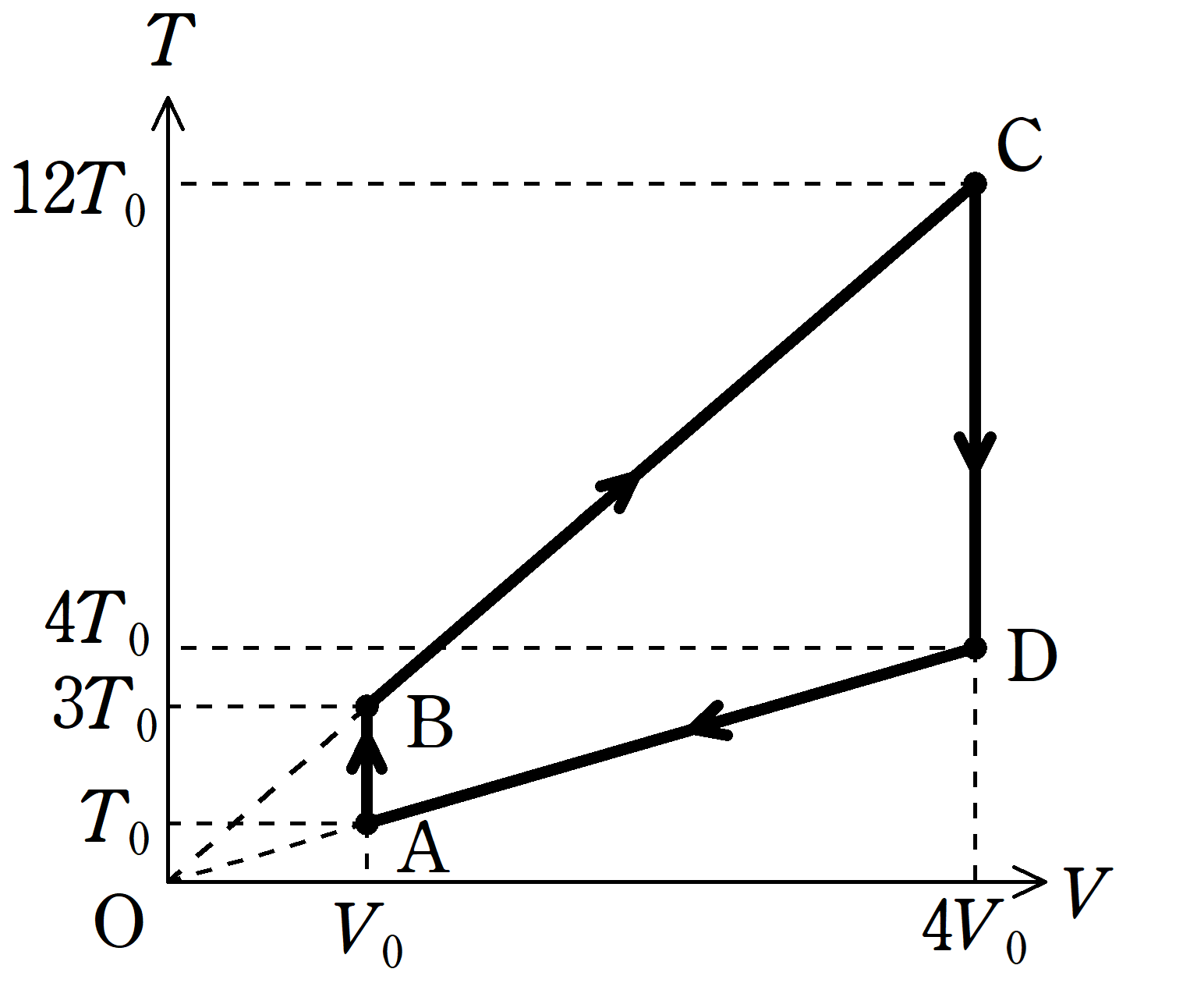
(2) 上図の$pV$図を縦軸が絶対温度$T$,横軸が体積$V$である$TV$図に書き直せ.
<解答>
(1)

絶対温度については,次のことを利用しましょう.
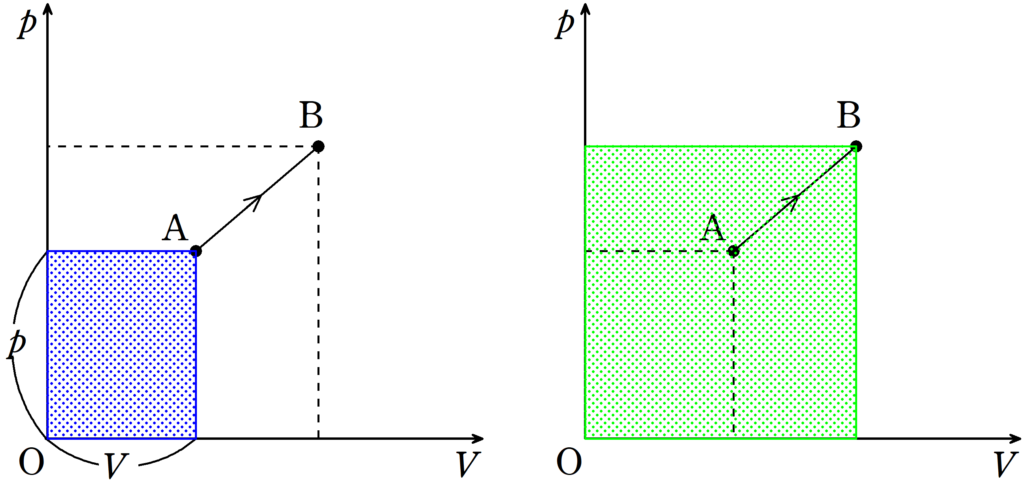
絶対温度は状態の点から$p$軸$V$軸へ下した垂線の足と原点でつくられる長方形の面積に比例する.
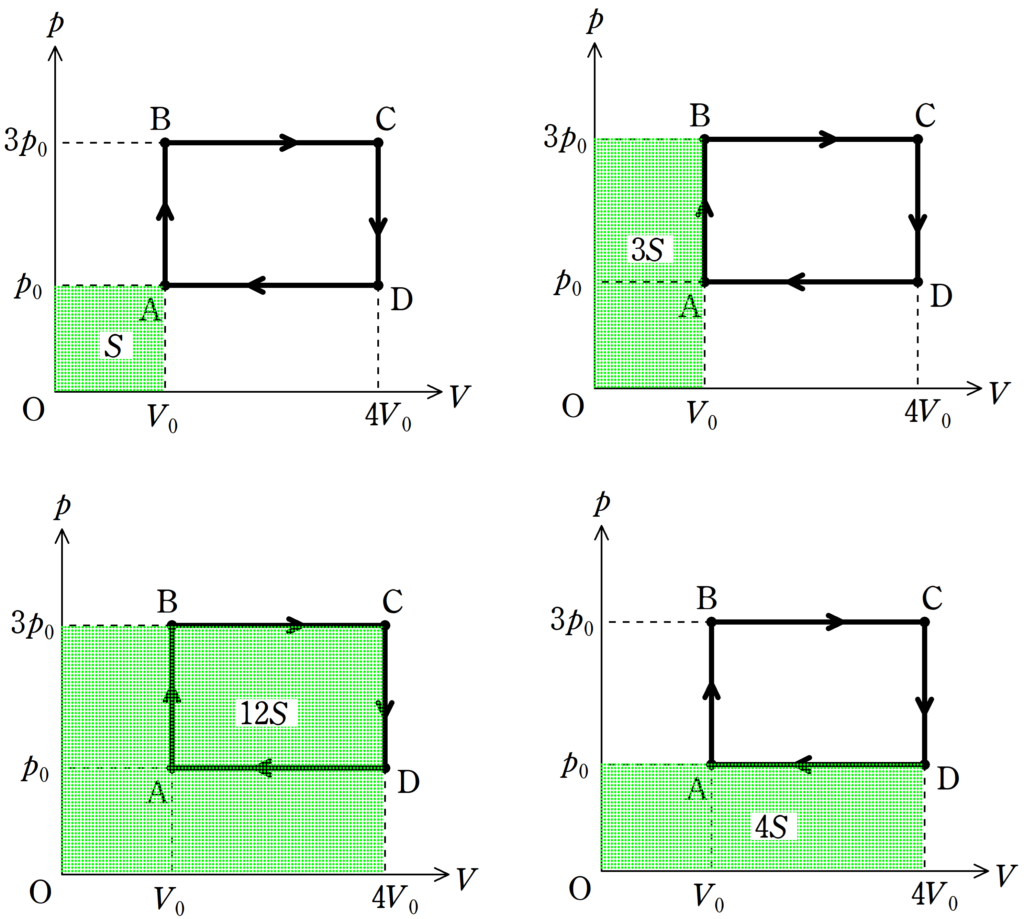

上図をみれば,Aの絶対温度が$T_{0}$なので,Bは3倍の$3T_{0}$,Cは$12T_{0}$,Dは$4T_{0}$となるね.
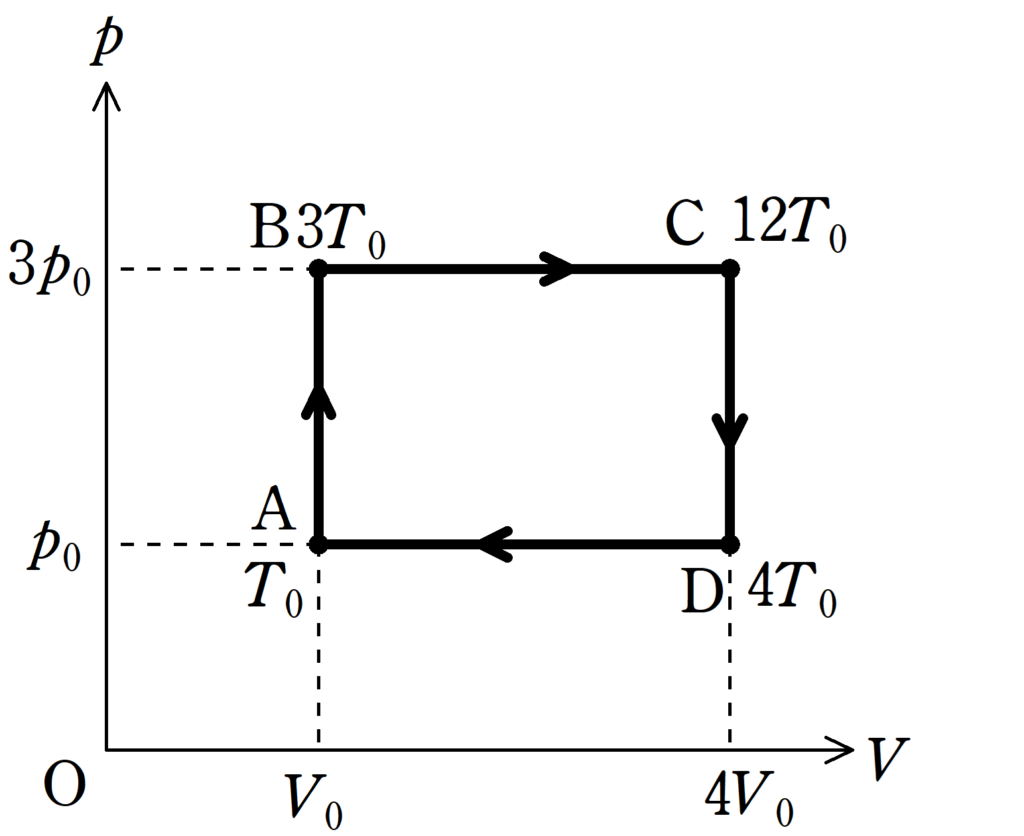
答え:$T_{\rm B}=3T_{0}$,$T_{\rm C}=12T_{0}$,$T_{\rm D}=4T_{0}$
(2)

さて,ここからが本題です.
まずは,状態Aから状態Bまでの変化を考えていきましょう.
状態Aから状態Bまでの変化は,定積変化です.
そして,絶対温度が上昇していくので,下図の青色部分のようになりますね.
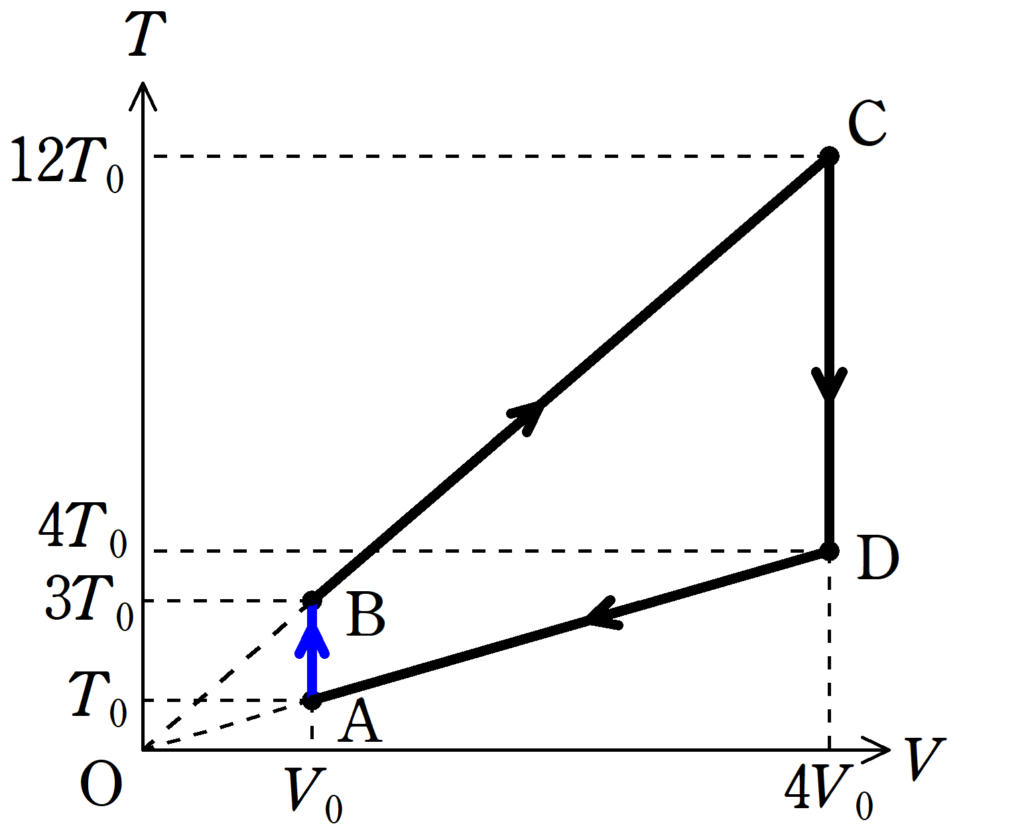

そして,状態Bから状態Cまでは定圧変化です.
定圧変化の$TV$図は次のようになります.
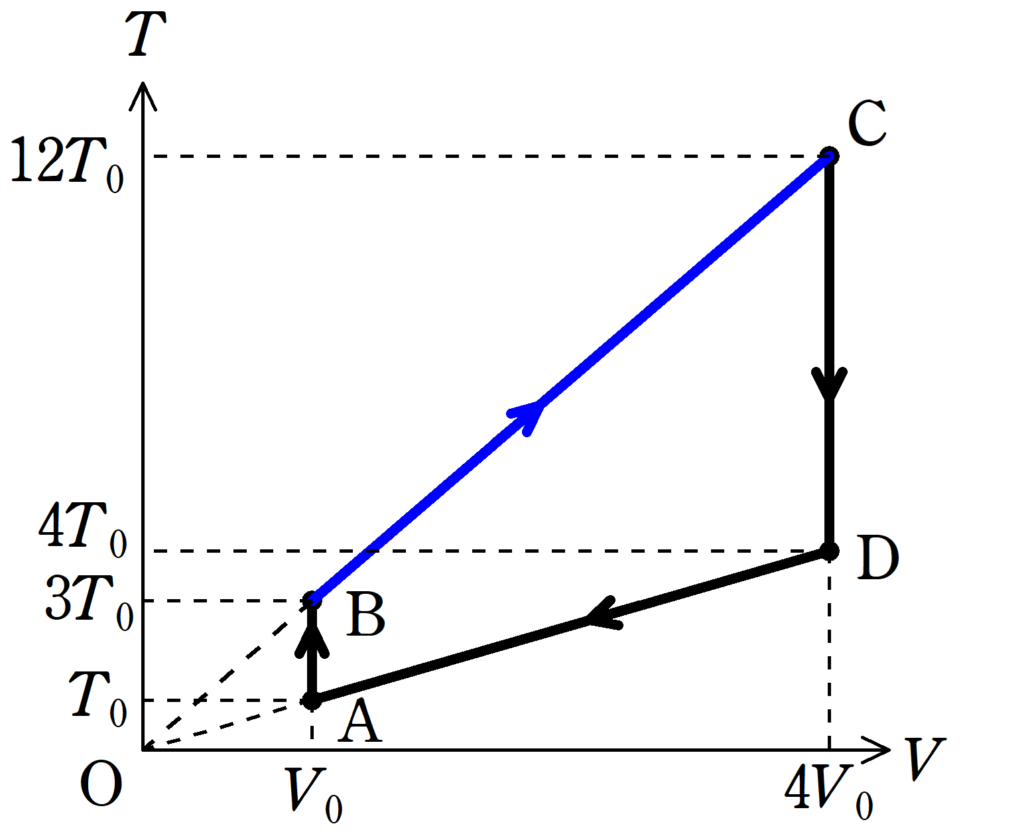

このとき,直線BCは原点を通ることに注意しましょう.
理由は次の通りです.
圧力$p$,物質量$n$が一定のとき,体積$V$,絶対温度を$T$,気体定数を$R$として,理想気体の状態方程式より
$p$$V$$=nR$$T$
$T$$=\dfrac{p}{nR}$$V$
これは,
$y$$=a$$x$
に対応させて考えれば,圧力が一定のとき,$TV$図のグラフは原点を通るような直線の一部であることがわかかる.

さらに,CからDの変化は体積を$4V_{0}$にしたまま,温度を下げていきます.
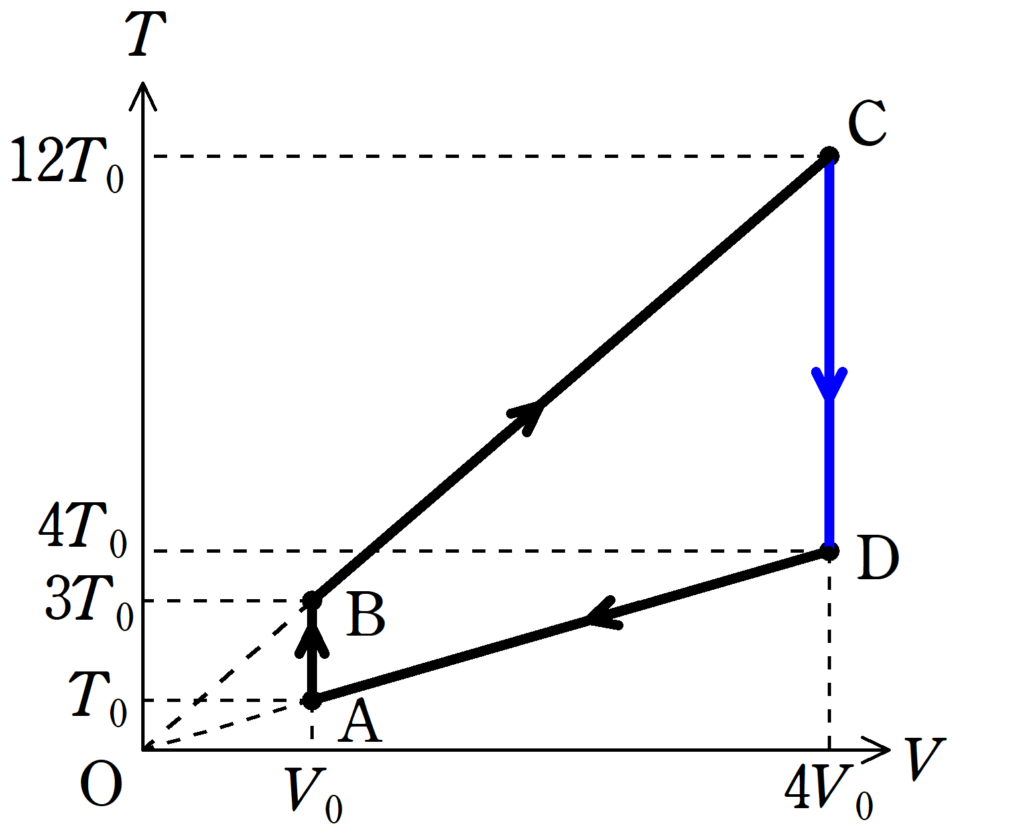

最後に,DからAも定圧変化なので,原点Oを通る直線の一部になっています.
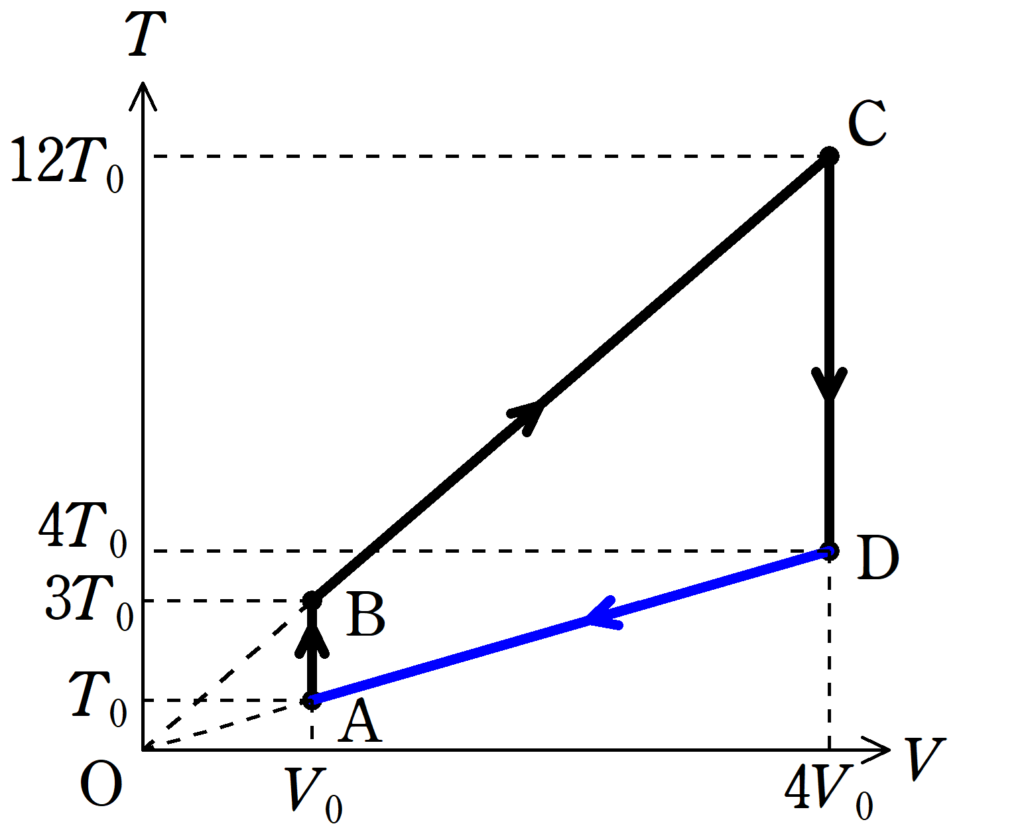

以上より,$TV$図は下のようになります.
BからCとDからAのグラフの鉛直線が原点Oを通っているところがポイントだね.

コメント