
前回の内容はこちらです.
前回は具体的な数値で計算しましたが,今回は文字を使った計算をしてみましょう.
今回使う物理公式,法則
- はね返り係数の式
- 力積と運動量変化の関係
- 作用・反作用の法則
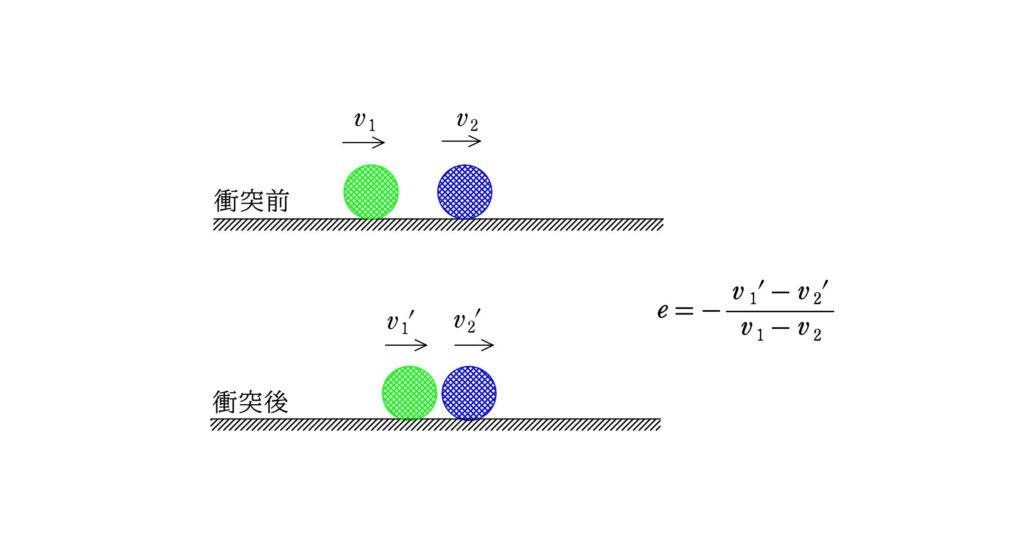
衝突前の物体の速度を$v_{1}$,$v_{2}$,衝突後の速度を$v_{1}^{\prime}$,$v_{2}^{\prime}$とするとき,はねかえり係数(反発係数)の式を次のように定義する.
$e=-\dfrac{v_{1}^{\prime}-v_{2}^{\prime}}{v_{1}-v_{2}}$
$e=1$のときを(完全)弾性衝突といい,力学的エネルギーが保存する.
また,$e=0$のときを完全非弾性衝突という.

特に今回は動かない壁との完全弾性衝突を考えます.すると,上の公式において,$e=1$,$v_{2}=v_{2}’=0$として
$1=-\dfrac{v_{1}’-0}{v_{1}-0}$
$\therefore\,\, v_{1}’=-v_{1}$
となり,動かない壁との完全弾性衝突では,衝突後の向きが衝突前と逆になり,速度の大きさは衝突直前後で変化しない,ということがわかります.
$(質量)\times (速度)$を運動量という.また,力が一定のとき,$(力)\times (力を受けた時間)$を力積という.
運動方程式を変形することによって,次の関係式を得ることができる.
運動量変化$=$力積

運動量は(質量)$\times $(速さ)ではなく,(質量)$\times $(速度)であることに注意しましょう.
物体Aが物体Bに力を及ぼしているとき,物体Bも物体Aに力を及ぼしている.それらの力は
- 同じ大きさ
- 力の作用線が一直線上
- 力の向きは反対
である.これを「作用反作用の法則」という.
壁に与えられた力積や平均の力を求める問題
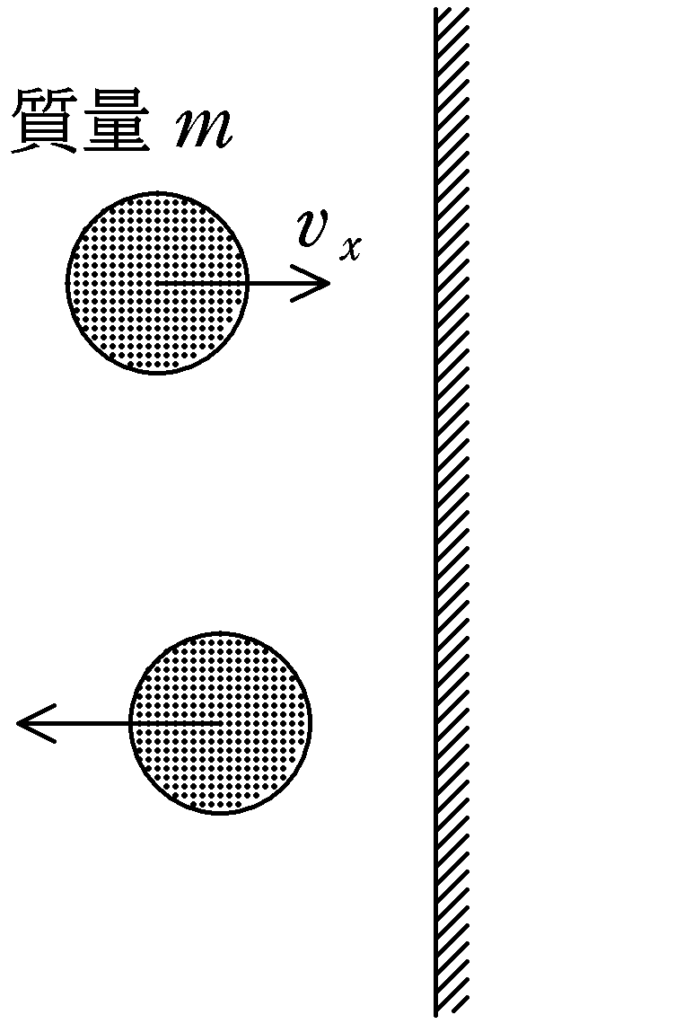
図のように,質量$m$の物体が速さ$v_{x}$で静止している壁と垂直に完全弾性衝突をした.次の問いに答えよ.
(1) 衝突直後の物体の速さを求めよ.
(2) 物体が壁と1回衝突した際に壁から受けた力積の大きさを求めよ.
(3) 物体が壁と1回衝突した際に壁が物体から受けた力積の大きさを求めよ.
(4) $\varDelta t$の間に同質量の物体が同じ速さで$A$回衝突した.この間に壁が受けた力積の和を求めよ.
(5) (4)のとき,壁が受けた平均の力の大きさを求めよ.
<解答>
(1)

さきほど考察したように,衝突直後の速さは変わらず,$v_{x}$
(答)のままです.
(2)

力積を直接計算することはできません.(力の大きさも衝突時間もわからないので)
そこで,
(力積)$=$(運動量変化) こちら
を用いて計算をしていきたいと思います.
衝突前の速度を正の方向とすると,衝突後の速度は$-v_{x}$なので,運動量は$m\times (-v_{x})=-mv_{x}$.また,衝突前の速度は$v_{x}$なので,運動量は$mv_{x}$です.したがって,運動量変化は
運動量変化$=-mv_{x}-(mv_{x})=-2mv_{x}$
となります.
したがって,物体の受けた力積の大きさは$2mv_{x}$(答)
(3)

壁が受ける力積の大きさは「作用反作用の法則」を使えばいいね.
物体が$2mv_{x}$の大きさの力積を受けるんだから,壁も$2mv_{x}$(答)の大きさの力積を物体から受けることになるね.
(4)

(3)で考えたように,1回衝突すると壁は$2mv_{x}$の大きさの力積を受けるんだから,$A$回衝突したら
$2mv_{x}\times A$(答)
の大きさの力積を受けるね.
(5)

最後に平均の力です.
(4)で$\varDelta t$の間に壁は$2mv_{x}\times A$の力積を受けることがわかりました.
力積$=$力$\times$時間
なので,平均の力の大きさを$F$として,
$2mv_{x}\times A=F\times \varDelta t$
$F=\dfrac{2mv_{x}A}{\varDelta t}$ (答)
と考えましょう.

文字の計算がわからなかったら,もう一度数値計算の問題を解いてみよう.



コメント