[演習]波の式が与えられたときの，波が伝わる速さの求め方

波動

2021.04.01

問題

位置$x$における時刻$t$の媒質の変位$y$が正の定数$A$，$B$，$C$を用いて

$y=A\cos(Bt+Cx)$　$\dots　(\spadesuit)$

と表される．

$(\spadesuit)$を満たす正弦波について，次の問いに答えよ．

(1)　正弦波の波長$\lambda$を$B$，$C$から必要なものを用いて表せ．

(2)　媒質の振動の周期$T$を$B$，$C$から必要なものを用いて表せ．

(3)　波の伝わる速度を$v$を$B$，$C$から必要なものを用いて表せ．ただし，$x$軸の正方向に波が伝わるとき，速度は正であるとする．

＜解答＞

(1)　

NEKO

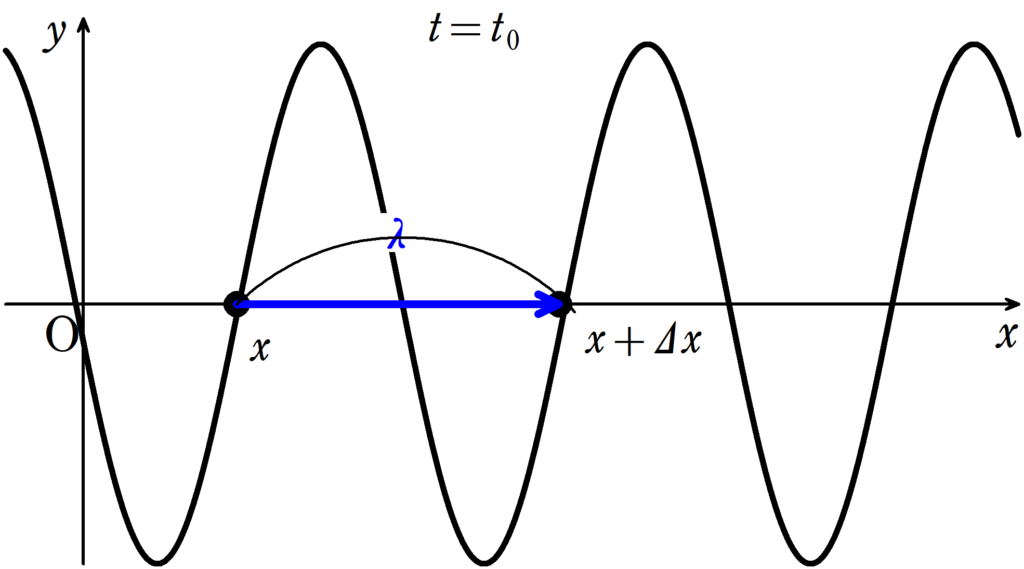
波長は波1個分の長さのことです．

時間を$t=t_{0}$と固定して位置を$x$から$x+\varDelta x$に変化させたときの$\cos$の中（位相といいます）の変化が$2\pi$になるときの$\varDelta x$が$\lambda$になります．

$\{Bt_{0}+C(x+\varDelta x)\}-(Bt_{0}+Cx)=2\pi$

$\therefore$　$C\varDelta x=2\pi$

$\varDelta x=\lambda$より

$\lambda=\dfrac{2\pi}{C}$　(答)

(2)　

NEKO

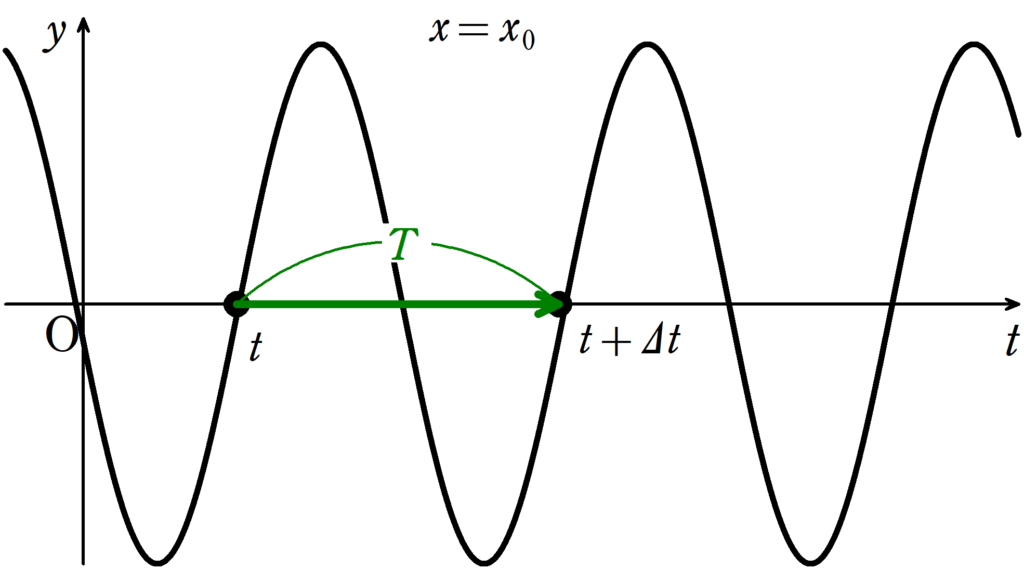
媒質の振動の周期は，媒質が1回振動するのにかかる時間です．

媒質の位置を$x=x_{0}$と固定して，$t$から$t+\varDelta t$と変化させたときの位相（$\cos$の中）の変化が$2\pi$であるときの$\varDelta t$が周期$T$です．

$\{B(t+\varDelta t)+Cx_{0}\}-(Bt+Cx_{0})=2\pi$

$\therefore$　$B\varDelta t=2\pi$

$\varDelta t=T$より

$T=\dfrac{2\pi}{B}$　(答)

(3)　

NEKO

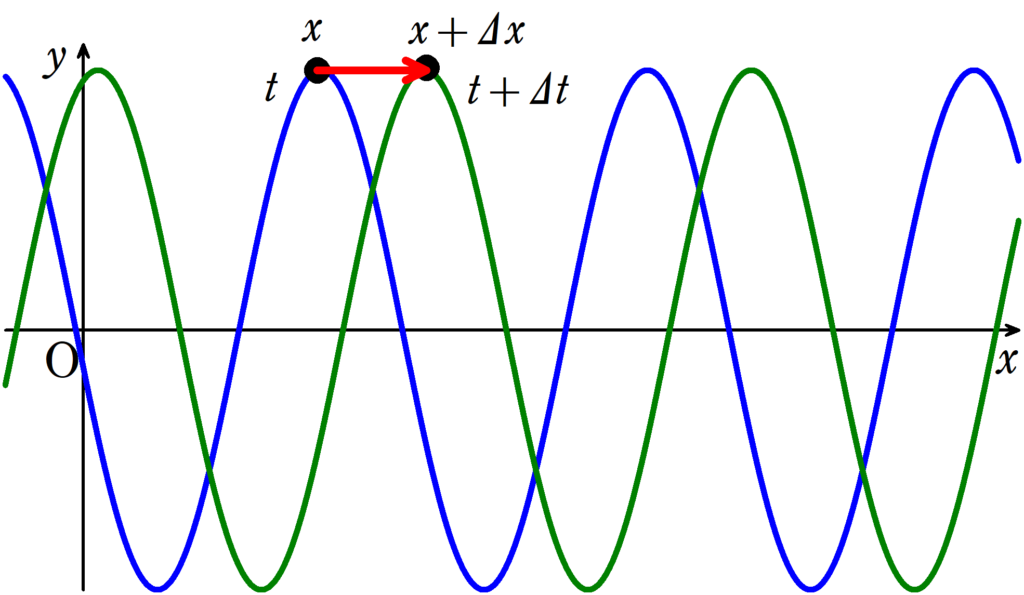
波が伝わる速度$v$は，時間$\varDelta t$経ったときに波が変化した位置を$\varDelta x$とするとき

$v=\dfrac{\varDelta x}{\varDelta t}$

です．

時刻が$t$から$t+\varDelta t$だけ変化して，同じ位相（上図では山部分）の部分が$x$から$x+\varDelta x$に変化したときに次の式が成り立ちます．

この2つが同位相（$\cos$の中が同じ）であることを利用して

$B(t+\varDelta t)+C(x+\varDelta x)=Bt+Cx$

$B\varDelta t+C\varDelta x=0$

$\dfrac{\varDelta x}{\varDelta t}=-\dfrac{B}{C}$

したがって，波の伝わる速度$v$は$v=-\dfrac{B}{C}$（答）