問題
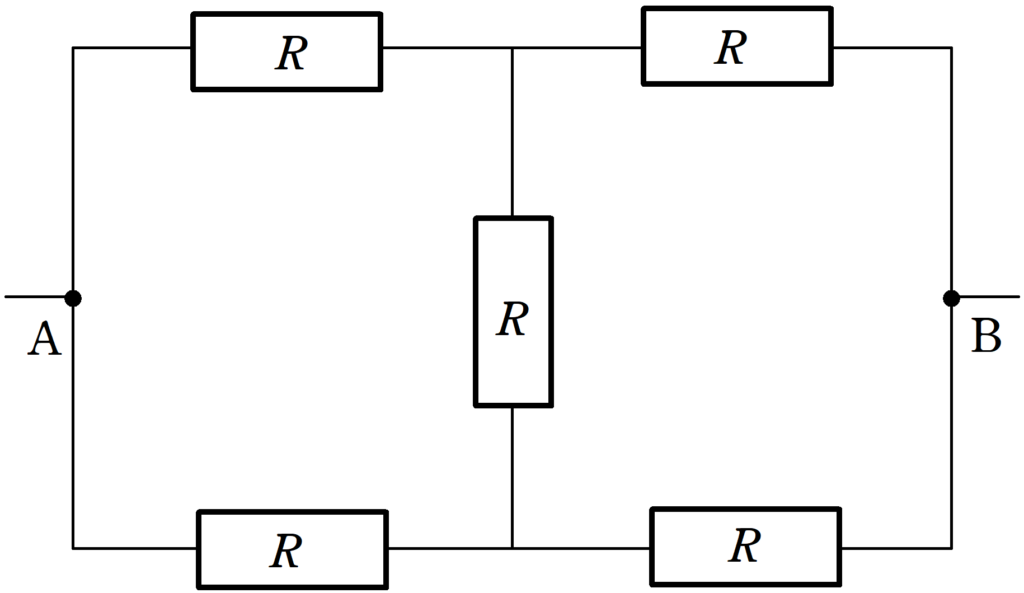
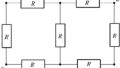
抵抗値$R$の5つの電気抵抗を上図のように,抵抗の無視できる導線で結んだ.
AB間の合成抵抗を求めよ.

PHYさん
抵抗は次のように定義しています.
オームの法則
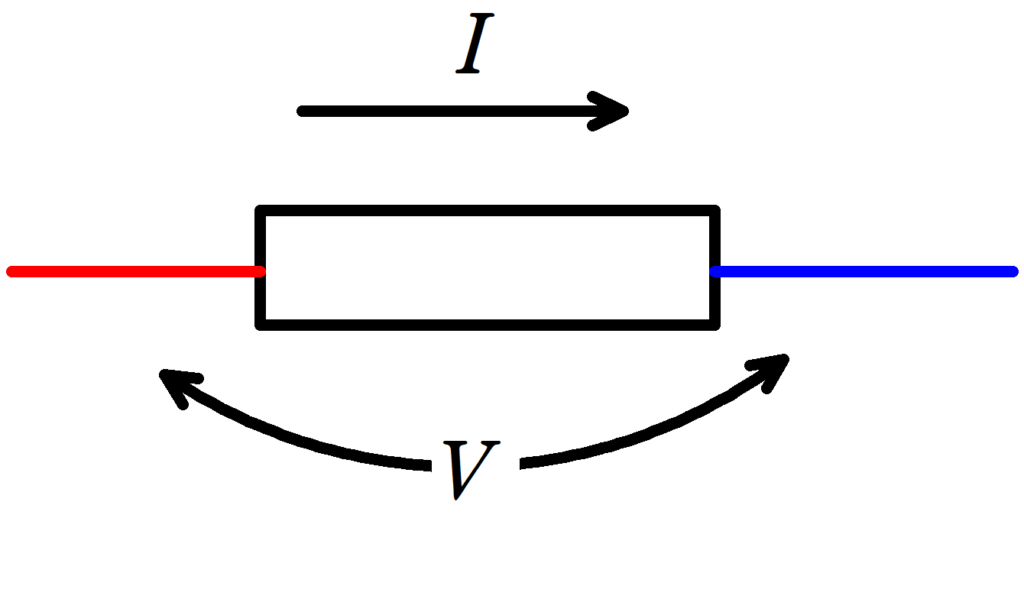
抵抗に流れる電流が$I$,電圧を$V$,抵抗値を$R$とするとき,
$V=RI$
が成り立つ.
合成抵抗を求めるときは,$\dfrac{V}{I}$を計算する.

PHYさん
Aから電流$I$が流れたときに,AB間にかかる電圧を$V$とします.
このとき,$\dfrac{V}{I}$の値がAB間の合成抵抗となります.

NEKO
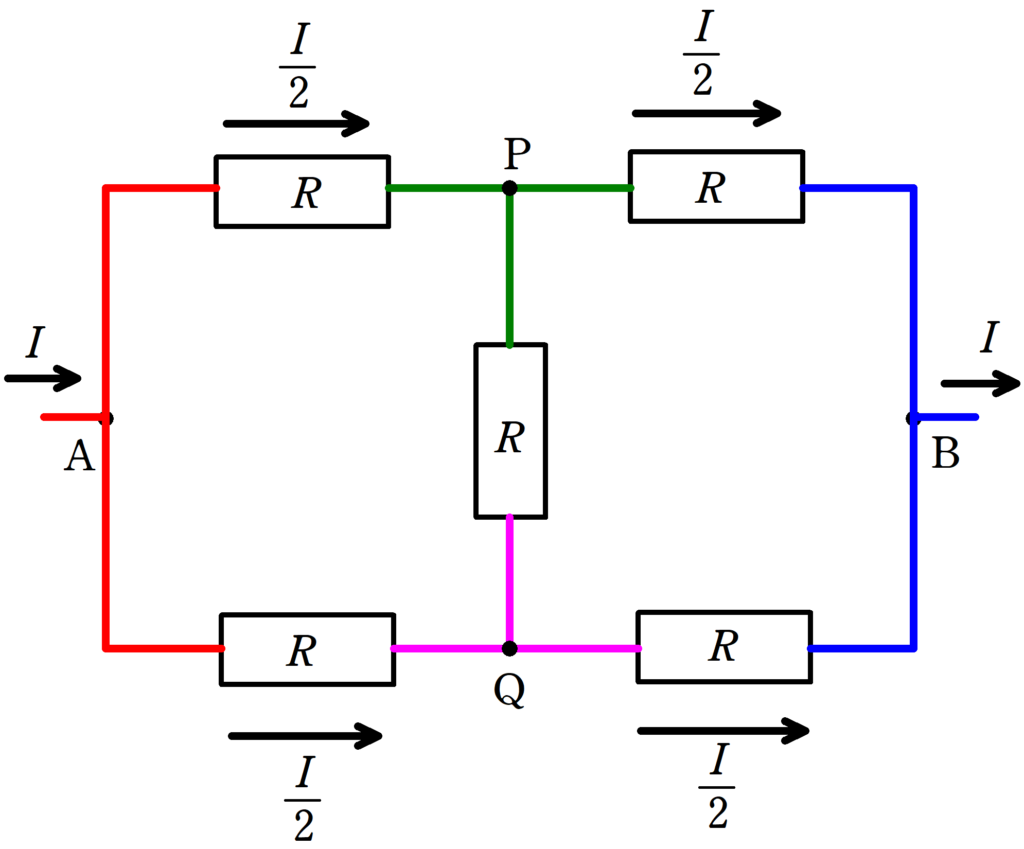
回路の対称性からAから電流$I$が流れ込んだとき,上図の上側と下側に$\dfrac{I}{2}$ずつ流れます.
また,キルヒホッフ第1法則より,Bから電流$I$が流れ出ていきます.
やはり,対称性からP→BとQ→Bに流れる電流はどちらも$\dfrac{I}{2}$になります.
その結果,PQ間には電流が流れないことが確認できます.
電圧降下の式を立てると次のようになります.
A→P→B経路を考えてみましょう.
★ 電圧降下の式(Bの電位を基準の0として,Aの電位を$V$とします)
$V-R\cdot \dfrac{I}{2}-R\cdot \dfrac{I}{2}=0$
$\therefore \dfrac{V}{I}=R$ (答)

NEKO
結果,合成抵抗は$R$ということがわかったね.


コメント
すみません問題に対しての質問なんですが、PQには電流は流れ込まないんですか?
対称性からPとQの電位差が生じないため,電流は流れません。
PQに電流が流れると仮定してキルヒホッフの第2法則を立てても確かめることができます。