
PHYさん
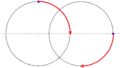
今回は,水面波が右から左に伝わっているとき,水面波の伝わる速さの半分のスピードで船が移動する様子の図をみていきましょう.
水面波が伝わる仕組みは,こちらでも説明しています.

NEKO
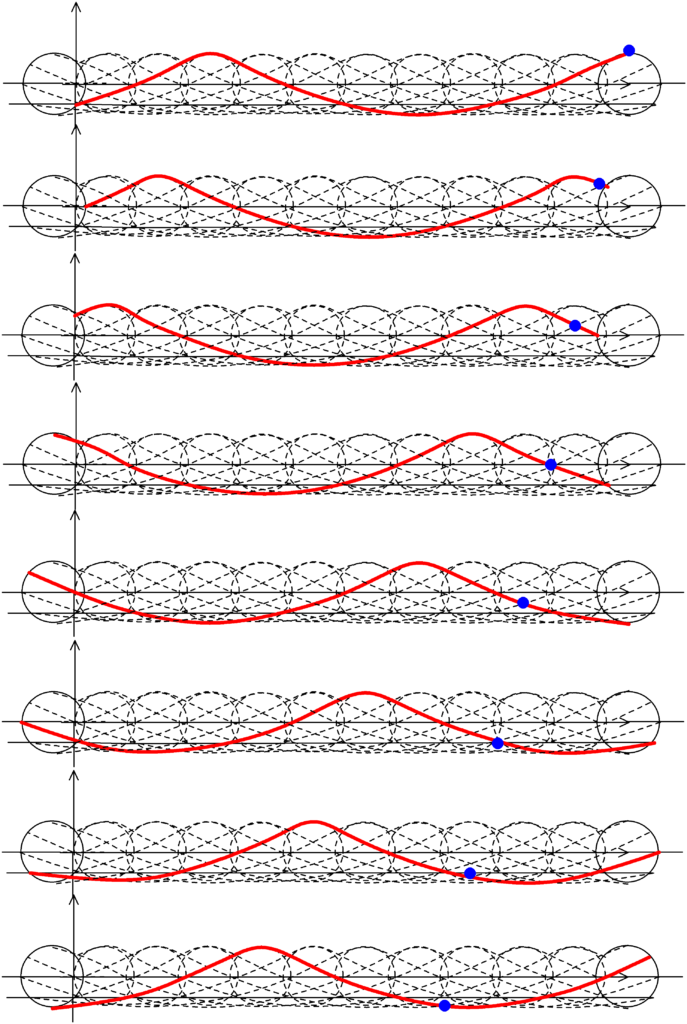
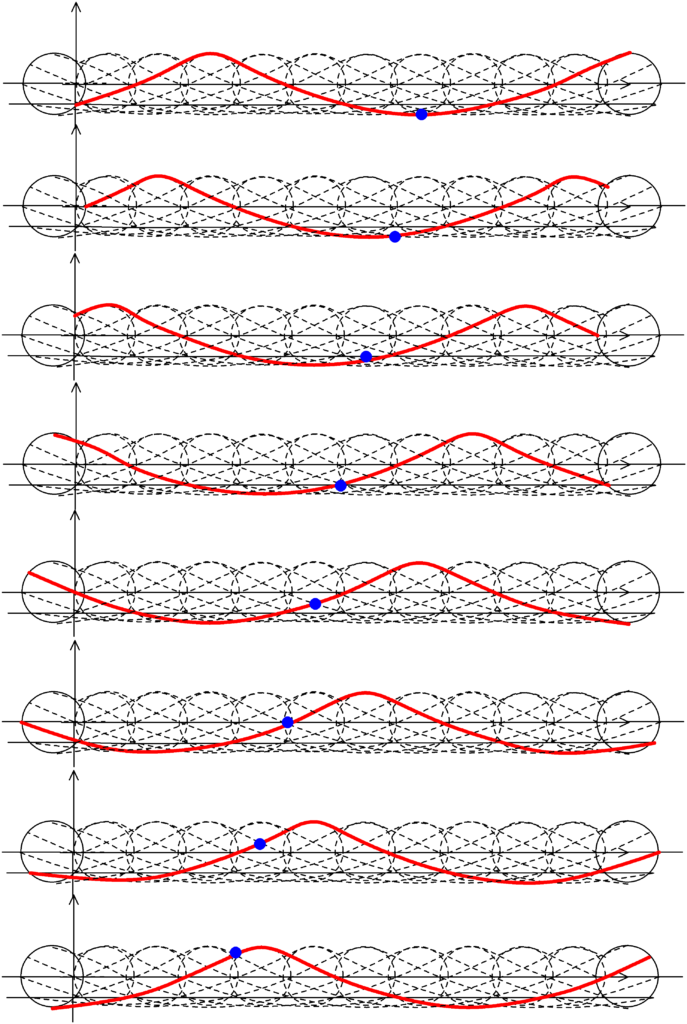
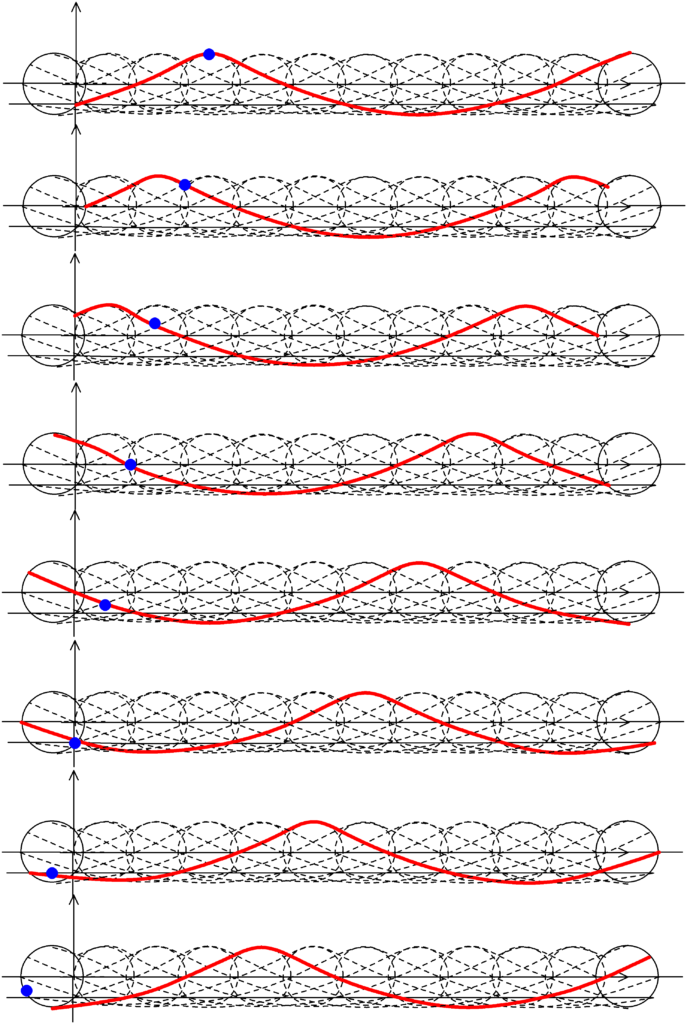
上図は,円運動の周期を$T$とすると,$\dfrac{1}{8}T$ごとの図になっているんだね.すると,船が再び一番高い場所にいくのにかかる時間は$\dfrac{16}{8}T=2T$になっているね.
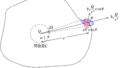
波の伝わる速さを$V$とすると,船の移動の速さが$\dfrac{V}{2}$になっているので,船に対する水面波の伝わる速さの相対速度は$V-\dfrac{V}{2}=\dfrac{V}{2}$になります.
波長は変化していないので,波の基本式($\lambda=VT$なので,)より,船にとっての波の周期$\tau$は,
$\lambda=\dfrac{V}{2}\tau$
$\therefore \tau =\dfrac{2\lambda}{V}=2T$
になるんだね.
もし,船の速度が$v(<V)$のときは,周期$\tau^{\prime}$は
$\lambda=(V-v)\cdot \tau^{\prime}$
$\therefore \tau^{\prime}=\dfrac{\lambda}{V-v}$
$\lambda=VT$なので,
$\tau^{\prime}=\dfrac{V}{V-v}T$
になるね.


コメント