
前回は,電流計とその1目盛りを変えるための抵抗である,分流器を扱ったね.
電圧計はどういう仕組みなの??

電圧計は電流計からつくることができます.
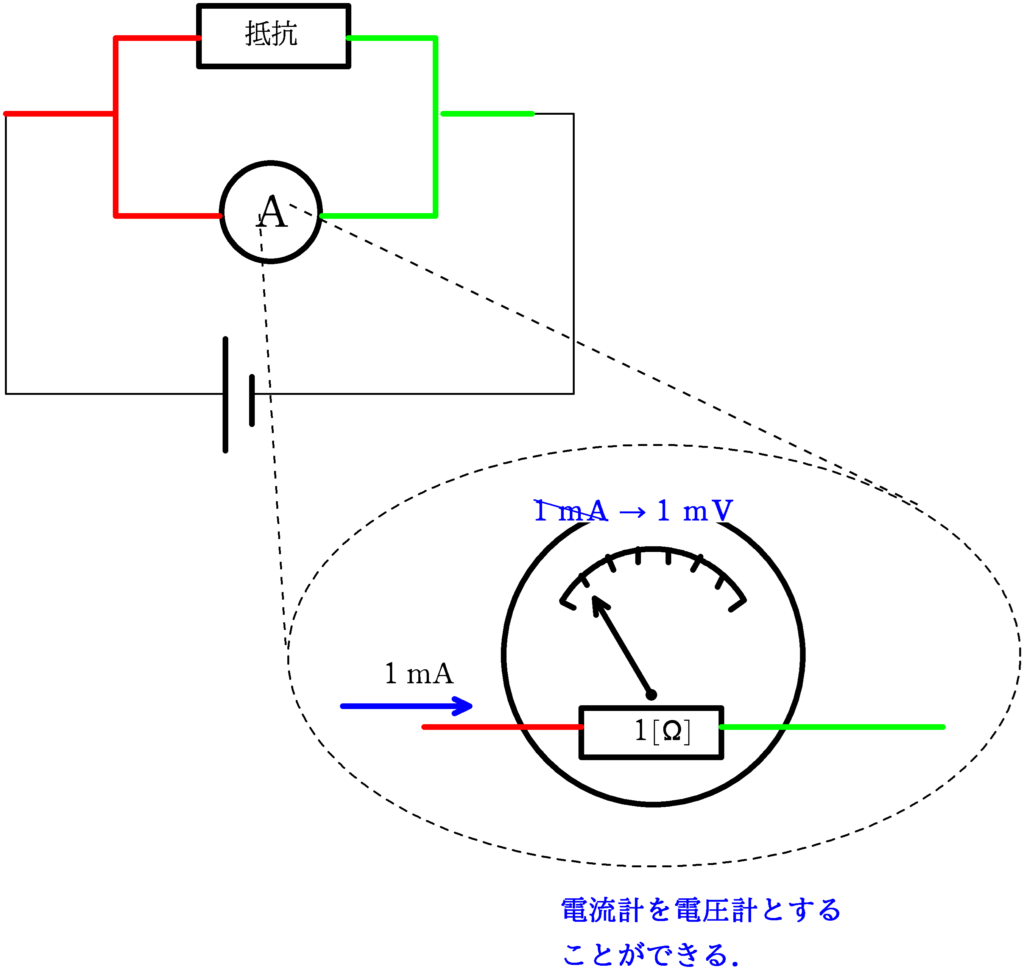

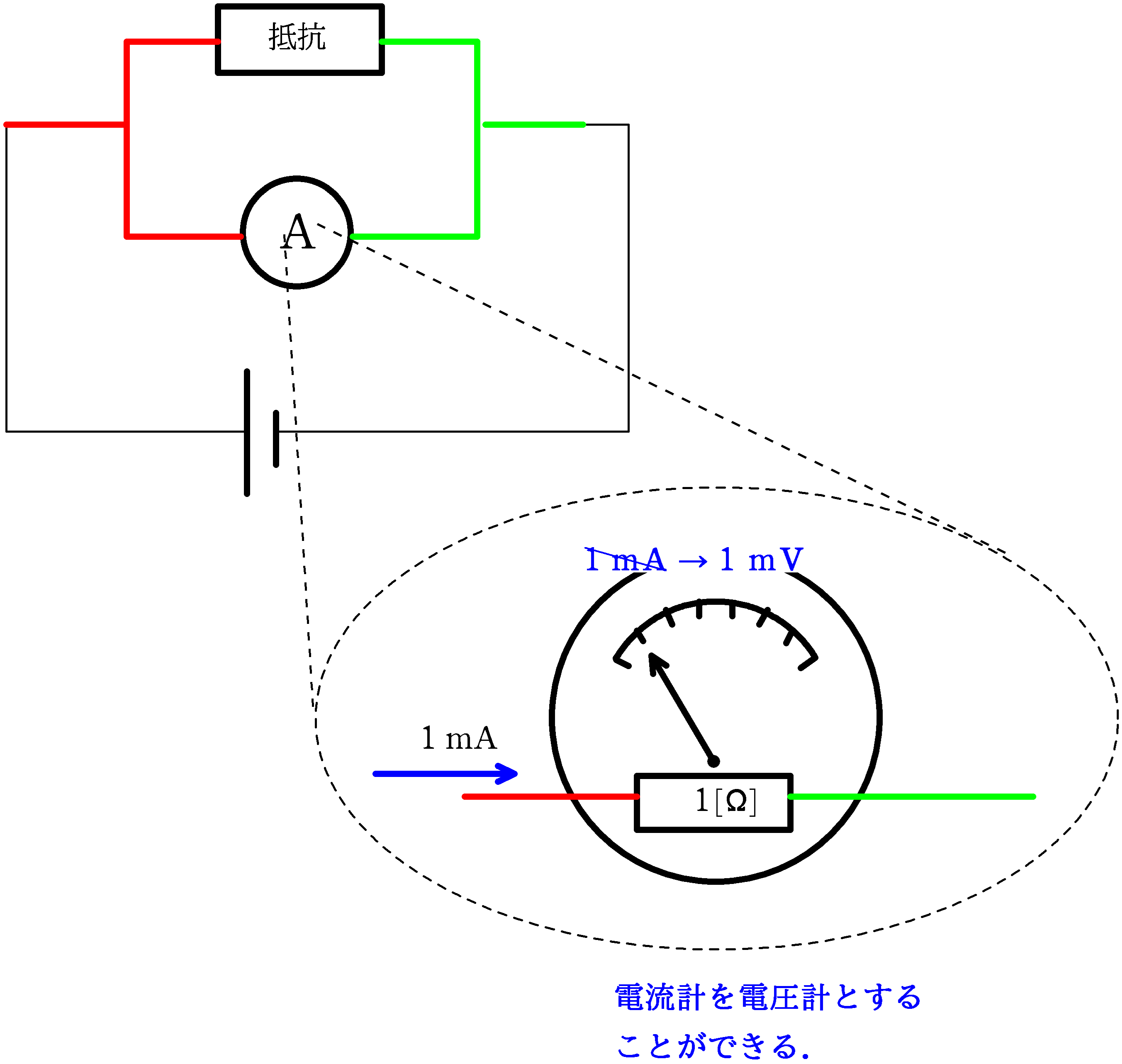
たとえば,1目盛り$1\,\rm mA$の電流計で,内部抵抗が$1\,\Omega$のとき,オームの法則で計算すると,このときの電流計の両端の電圧は
$1\cdot 1\times10^{-3}=1\,\rm mV$
となります.そこで,目盛りを修正液で消して(※もちろん実際はそんなことしません)
$1\,\rm mA$ を $1\,\rm mV$
とすればいいんです.

なるほど,じゃあ,そのように作った電圧計の1目盛りを変えるにはまた,別な抵抗をつなげてあげればいいのかな??

その通りです.
ただ,電圧計の1目盛りを変えるためには,抵抗を直列につなぎます.
もともと1目盛り$V_{0}\,[\rm V]$の電流計を$x$倍の$xV_{0}\,[\rm V]$にする場合はどのように考えればいいと思いますか?
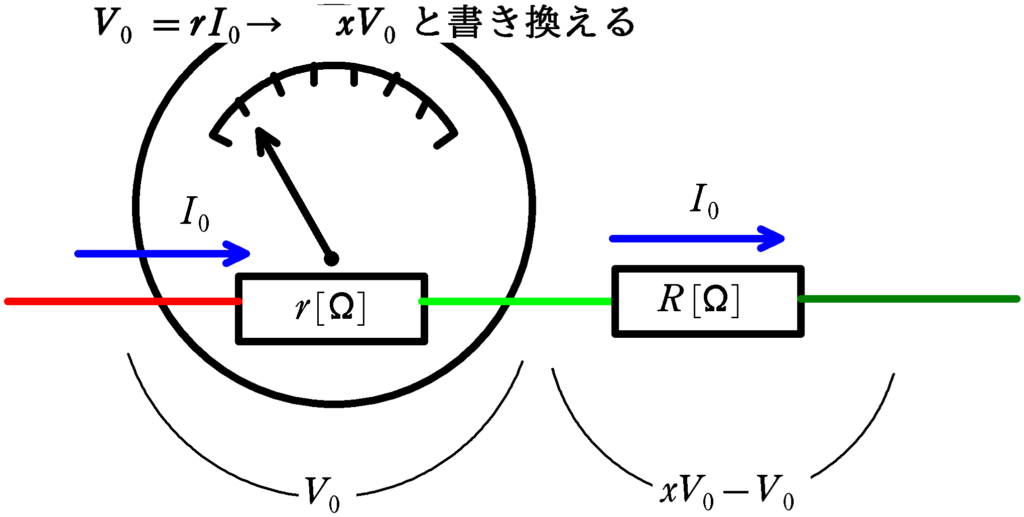

たとえば,電圧計の内部抵抗を$r\,\Omega$として,1目盛り分の電流($I_{0}\,[\rm A]$とする)が流れると電圧が$V_{0}\,[\rm V]$落ちるとすると,残りの電圧
$xV_{0}-V_{0}\,[\rm V]$
は直列につないだ抵抗$R\,[\Omega]$で落ちればいいんだね.
2つの抵抗でオームの法則を立てると
★ オームの法則
$V_{0}=rI_{0} \cdots (\ast)$
$(x-1)V_{0}=RI_{0} \cdots (2\ast)$
$(\ast)$を$(2\ast)$に代入して$V_{0}$を消去すると
$(x-1)r\cancel{I_{0}}=R\cancel{I_{0}}$
$\therefore R=(x-1)r$

つまり,電圧計の抵抗と直列に$R=(x-1)r\,[\Omega]$の抵抗をつなげば1目盛りが$x$倍になるんだね.

そういうことです.ちなみにこの抵抗$R\,[\Omega]$の抵抗を倍率器といいます.
倍率器の抵抗も分流器と同様に覚えるのではなく,電流や電圧を設定して計算した方がよいかと思います.
内部抵抗$1\,\Omega$で1目盛り$1\,\rm mA$の電流計がある.これを1目盛り$1\,\rm V$の電圧計にするには,何$\Omega$の抵抗をどのように(直列か並列か)接続すればよいか.
<解答>

$1\,\rm mA$の電流が流れると$1$目盛り分触れるということは,オームの法則より,1目盛りが
$1\,[\Omega]\cdot 1{\rm m}[\rm A]=1\,\rm mV$
の電圧計ということでもあるね.
これを1目盛り$1\,\rm V$つまり$1000\,\rm mV$の電圧計にするためには,直列(答)に抵抗をつないで,その抵抗で残りの$999\,\rm mV$を落とせばいいだね.
その抵抗$R\,[\Omega]$として,オームの法則を立ててみましょう.
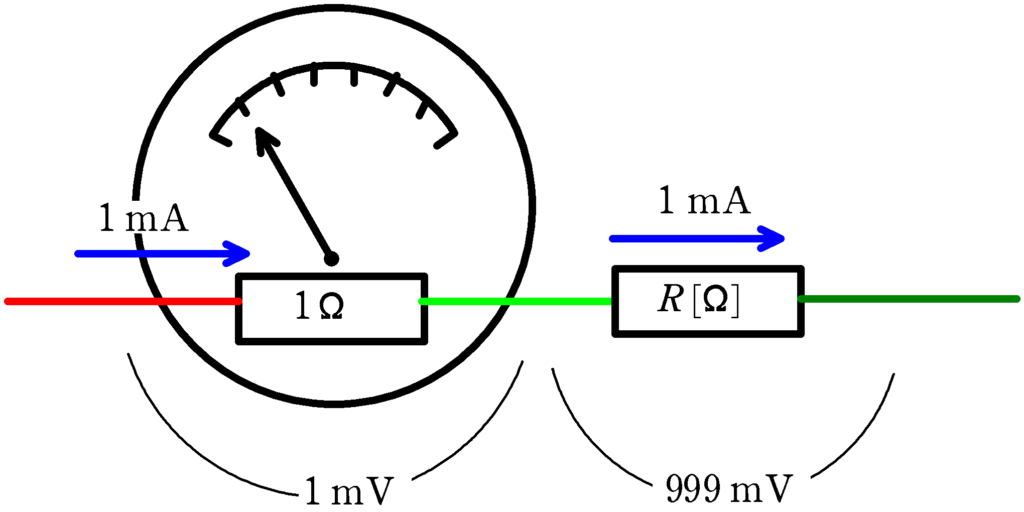
★ 倍率器(抵抗$R\,[\Omega]$)でのオームの法則
$999\cancel{\rm m}[\rm V]=R\,[\Omega]\times 1\cancel{\rm m}[\rm A]$
$\therefore R=999\,\Omega$ (答)

コメント