
今回は熱力学の演習問題です.
入試では,
定圧変化,定積変化,等温変化,断熱変化
は頻出の変化ですが,それ以外もある程度経験しておいた方がいいと思います.
具体的には
- ばねつきピストン
- ピストンの上の液体の量が変化する問題
- 2つの容器と連結棒の問題
いずれも,一筋縄ではいきませんが,一つ一つ攻略していきましょう.
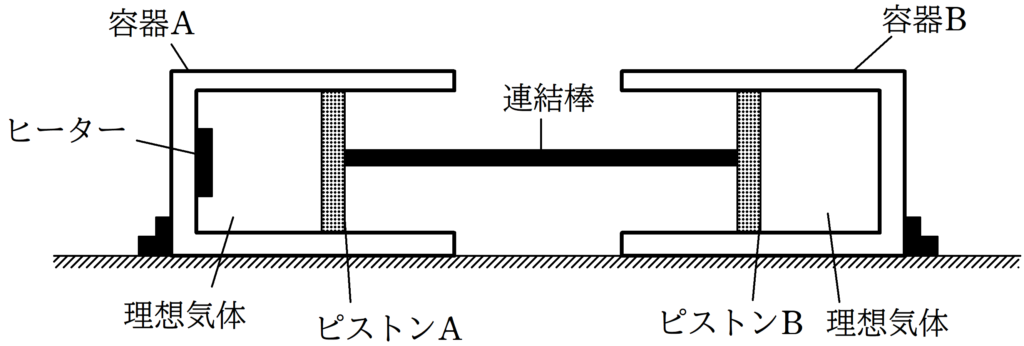
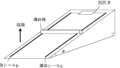
上図のように,水平な床の上に同じ形,大きさの容器A,Bがある.
容器A,B内にある理想気体はピストンA,Bによって封入されている.
また,ピストンA,Bは軽くて変形しない連結棒によってつながっている.
容器A,BとピストンA,Bは断熱材でできており,ピストンは水平方向になめらかに動くとしてよい.
はじめ,容器A,B内の理想気体の圧力,体積,絶対温度はそれぞれ$p_{1},V_{1},T_{1}$であった.
この状態から容器Aにあるヒーターによって,容器A内の理想気体をあたためたところ,ピストンA,連結棒,ピストンBは図の右方向へ移動して,容器A内の理想気体の体積が$\dfrac{3}{2}V_{1}$になったとことろでヒーターを止めた.
また,断熱変化については,圧力を$p$,体積を$V$,比熱比を$\gamma$として,次の式が成り立つことを用いてよい.
$pV^{\gamma}=$一定
(1) 容器Aの体積が$\dfrac{3}{2}V_{1}$になったときの容器A内の圧力を$p_{\rm{A}}$,絶対温度を$T_{\rm{A}}$,容器B内の圧力を$p_{\rm{B}}$,絶対温度を$T_{\rm{B}}$とする.$p_{\rm{A}} , p_{\rm{B}} , T_{\rm{A}},T_{\rm{B}}$を求めよ.ただし,使用する文字は$p_{1} , T_{1} , \gamma$のみとする.
(2) 縦軸を圧力$p$,横軸を体積$V$として,容器Aの気体の体積が$V_{1}$から$\dfrac{3}{2}V_{1}$になるまでの,容器A内にある気体と容器B内にある気体それぞれの$p-V$グラフの概形をかけ.
<解答>

熱力学の問題は次の3つの式を思い出そう!
今回は「1.」と「2.」を使うよ.
- 可動部分のつり合いの式 → 力の情報が出てくる
- 理想気体の状態方程式(ボイルシャルルの法則)
- 熱力学第一法則 → エネルギーの情報が出てくる

では,問題文の情報を整理する作業からしましょう.
ここができていないと何の式を立てればいいのか見通しがたたないので,丁寧にかこう!
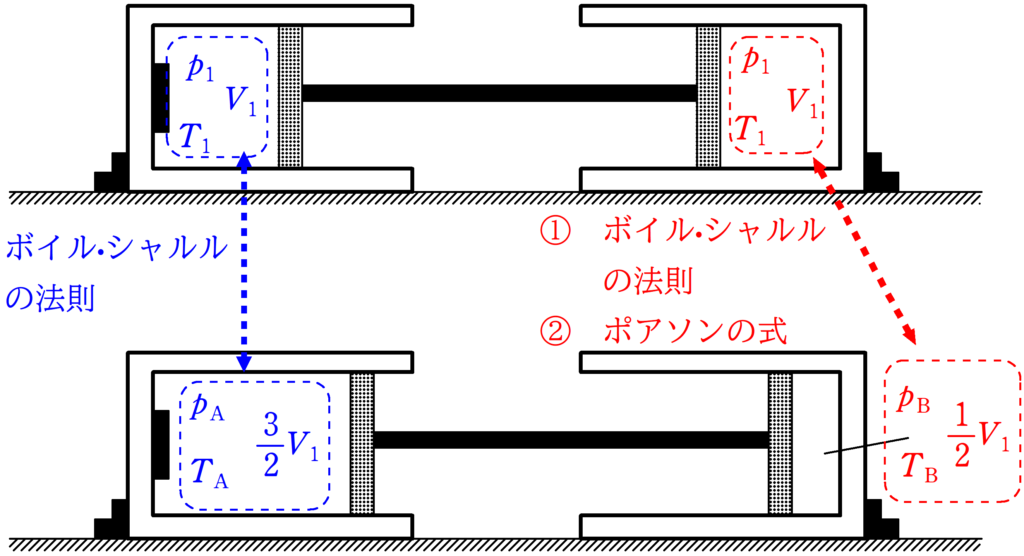

容器A内の気体を気体A,B内の気体を気体Bと呼びます.
気体Aの体積が$\dfrac{1}{2}V_{1}$増えているので,その分気体Bの体積が$\dfrac{1}{2}V_{1}$減っているんだね.

気体Aの物質量は変化していないね.
なので,ボイル・シャルルの法則が成り立ちます.
同じく,気体Bの物質量も変化していないので,ボイル・シャルルの法則を立てることができるよ.
$\dfrac{p_{1}V_{1}}{T_{1}}=\dfrac{p_{\rm{A}}\dfrac{3}{2}V_{1}}{T_{\rm{A}}}$
$\therefore$ ${T_{\rm{A}}}$$=\dfrac{3T_{1}}{2p_{1}}$$p_{\rm{A}}$ $\dots (\ast)$
$\dfrac{p_{1}V_{1}}{T_{1}}=\dfrac{p_{\rm{B}}\dfrac{1}{2}V_{1}}{T_{\rm{B}}}$
$\therefore$ $T_{\rm{B}}$$=\dfrac{T_{1}}{2p_{1}}$$p_{\rm{B}}$ $\dots (2\ast)$

しかし,これだけでは解けないね.
なぜかというと,今回(1)で求めるのは
$p_{\rm{A}},p_{\rm{B}},T_{\rm{A}},T_{\rm{B}}$の4つの未知な文字があるからです.
普通,4つの未知な文字があったら,4つの式が必要です.

そこで,気体Bに着目します.
ピストンも容器Bも断熱材によってできていることと,ヒーターなどで熱を吸収しているわけでもないので,断熱変化をします.
したがって,ポアソンの式より
$p_{1}V_{1}^{\gamma}=p_{\rm{B}}\cdot(\dfrac{1}{2}V_{1})^{\gamma}$
$p_{1}\cancel{V_{1}^{\gamma}}=p_{\rm{B}}\dfrac{1}{2^{\gamma}}\cancel{V_{1}^{\gamma}}$
$\therefore$ $p_{\rm{B}}$$=2^{\gamma}p_{1} \dots (3\ast)$

そして,可動部のつり合いの式です.
連結棒と2つのピストン全体を対象としましょう.
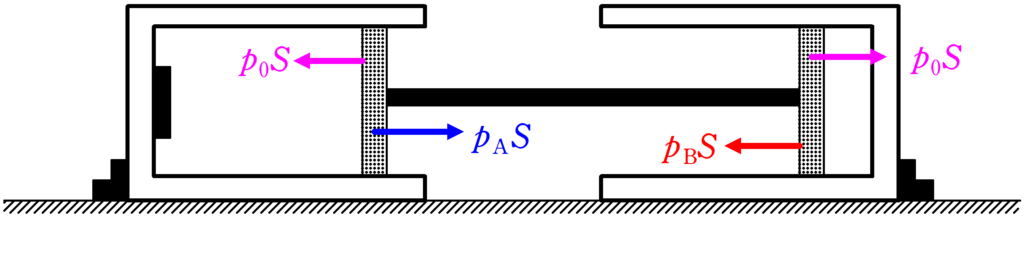

上図では外気圧を$p_{0}$,ピストンの断面積を$S$としたよ.
どのみち,外気圧はピストンA,ピストンBどちらにもかかるからプラスマイナス0になるね.
ということは,次のような関係が成り立ちます.
$p_{\rm{A}}$$=$$p_{\rm{B}}$ $\dots (4\ast)$

ちなみに,ピストンAだけに着目して,$p_{\rm{A}}=p_{0}$!という人がいるけど,これは間違いだよ.
なんで間違いかわかるかな?

ピストンAだけを対象にすると,連結棒からの抗力を考えないといけないからです.
つまり,未知な力が出てくるので,連結棒やピストンBに関してもつり合いの式を立てる必要があります.
そうすることで,結局同じ答えになるよ.
では,答えを出しましょう.
$(3\ast)$より,$p_{\rm{B}}$$=2^{\gamma}p_{1}$(答)なので,$(4\ast)$より
$p_{\rm{A}}$$=2^{\gamma}p_{1}$(答)
さらに,これらを$(\ast)$と$(2\ast)$に代入して
$T_{\rm{A}}$$=\dfrac{3T_{1}}{2\cancel{p_{1}}}2^{\gamma}\cancel{p_{1}}=3\cdot2^{\gamma -1}T_{1}$(答)
$T_{\rm{B}}$$=\dfrac{T_{1}}{2\cancel{p_{1}}}2^{\gamma}\cancel{p_{1}}=2^{\gamma -1}T_{1}$(答)
(2)

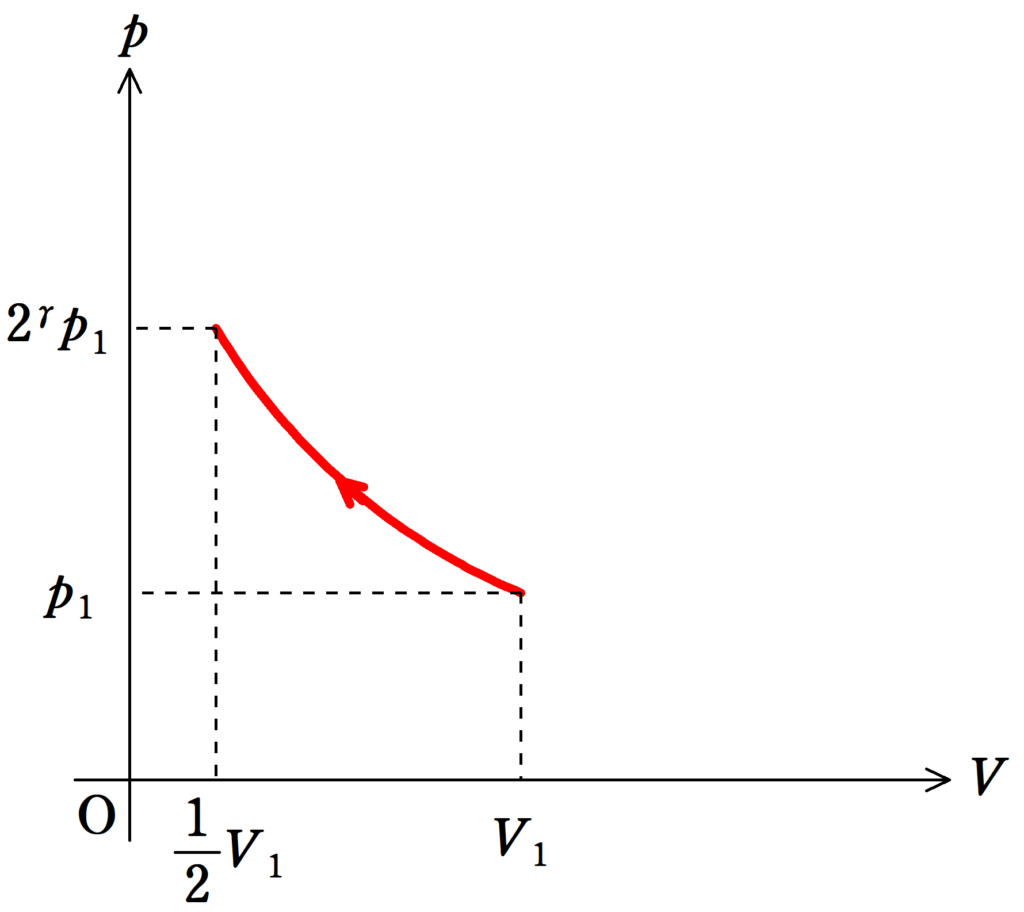
まず,断熱変化である気体Bの方$p-V$グラフは下のようになるね.
Bは断熱圧縮といわれて,熱を遮断しながら,圧縮すると圧力,温度ともに高くなります.
曲線になるのは,$C$を定数とすると,ポアソンの式より
$pV^{\gamma}=C$
$p=\dfrac{C}{V^{\gamma}}$
となるからだよ.

ここで,Aの気体とBの気体の圧力は常に等しいことに着目しましょう.
$(4\ast)$からすぐわかるね.
Aの体積が$\Delta V$増加するとき,Bの体積は$\Delta V$減少します.
このときの圧力が等しいことからAの気体の$p-V$グラフは,Bの$p-V$グラフを$V=V_{1}$について折り返したグラフになります!
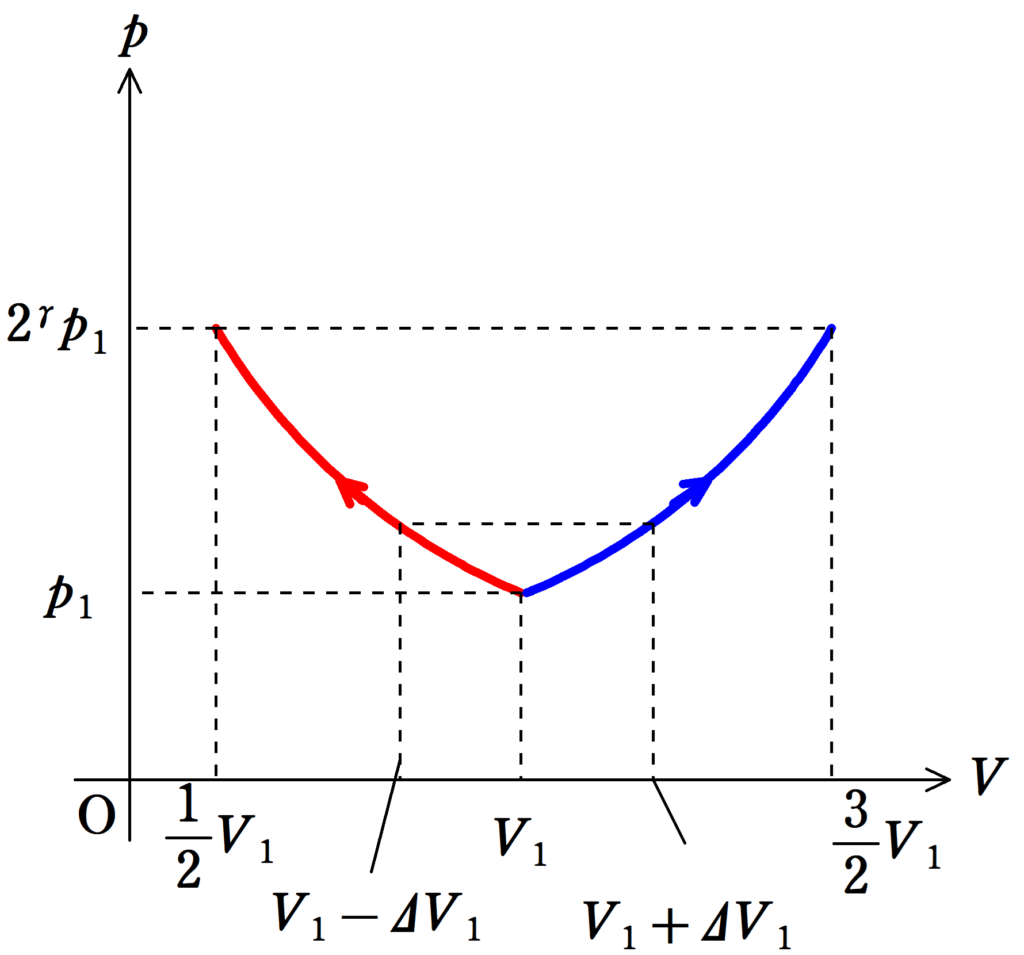

このように,断熱変化のグラフを折り返したグラフになる$p-V$グラフも出てきます.




コメント
[…] […]
[…] […]