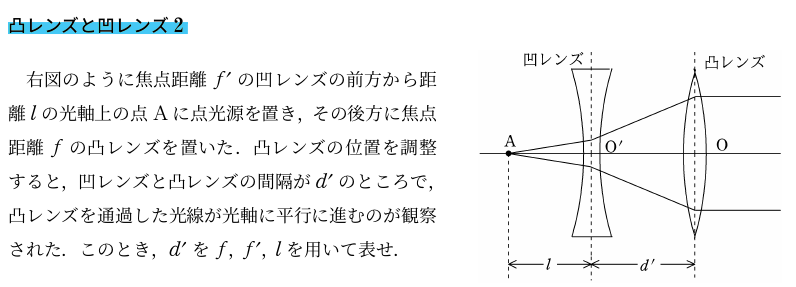
<問題>
<解答>
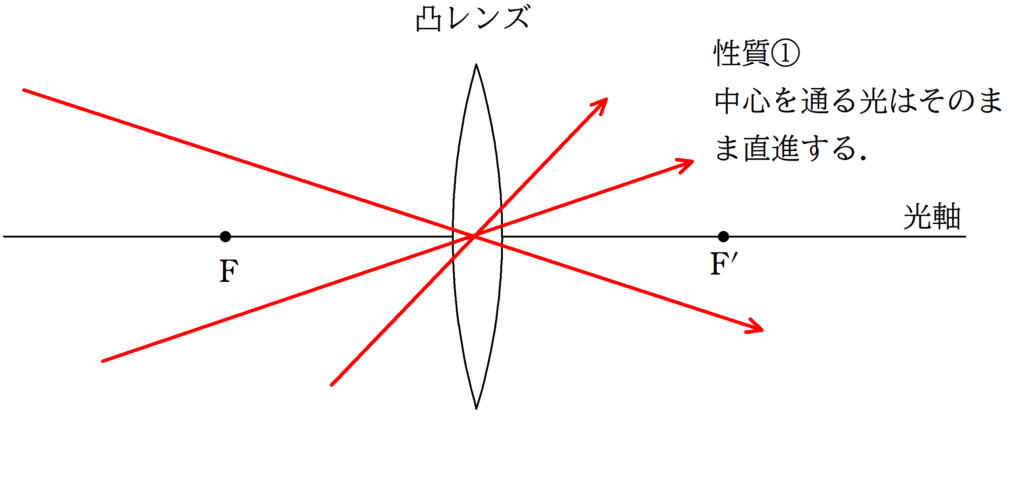
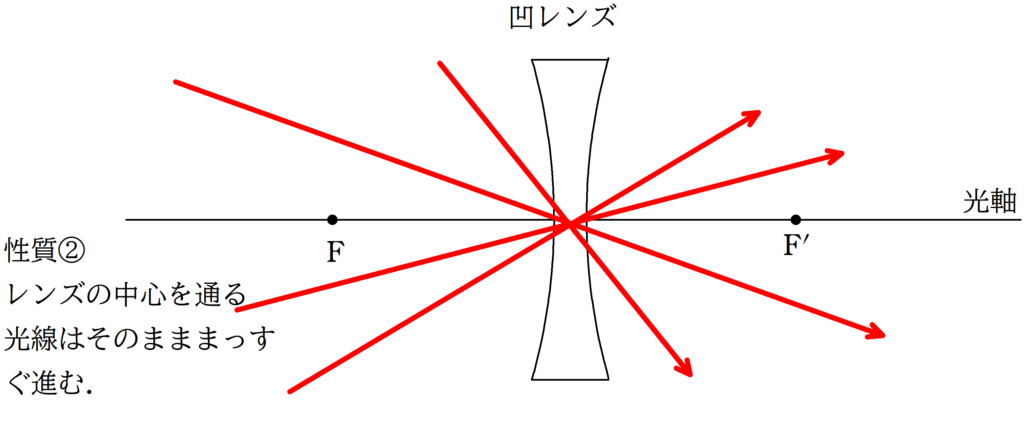
まず,凸レンズの代表光線を確認しましょう.
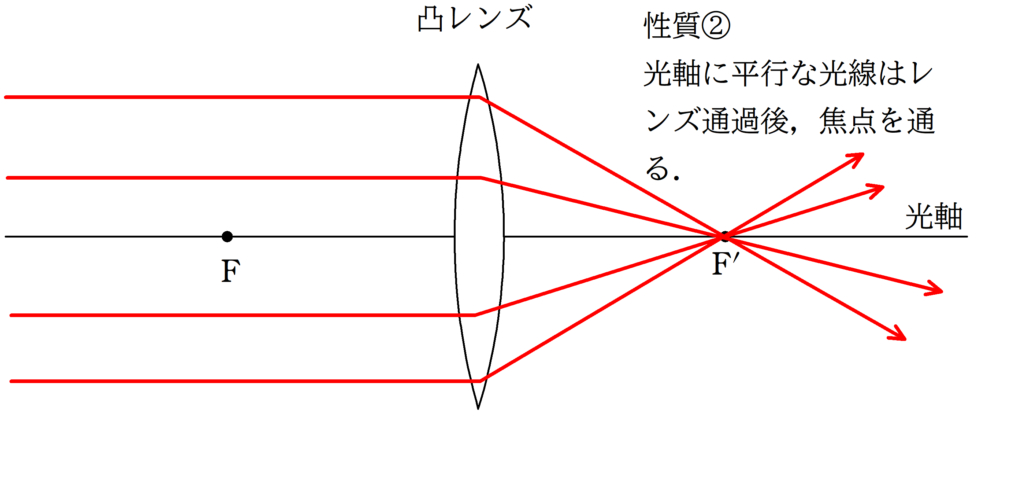
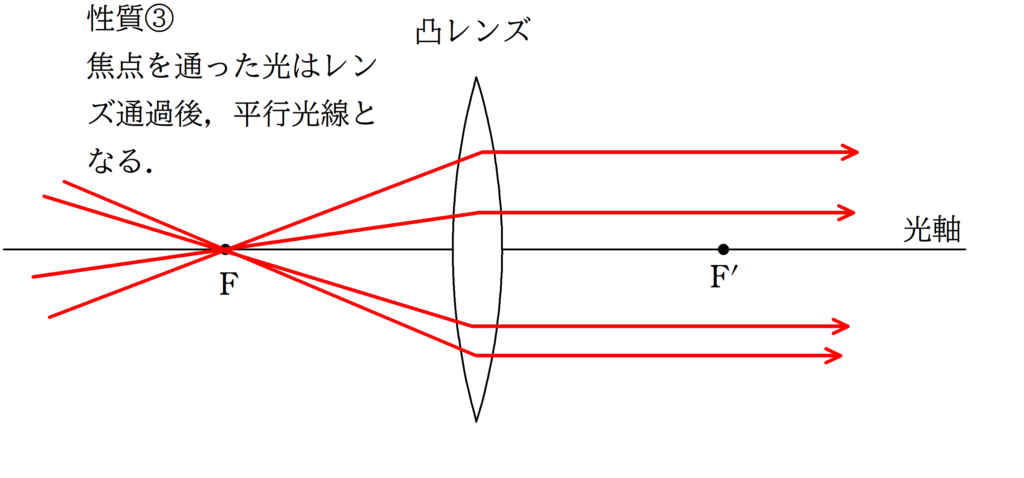
性質③より,「焦点を通った光はレンズ通過後,平行光線となる.」ということから,凸レンズの焦点は下図の点$\rm B$であることがわかり,${\rm BO}=f$となります.
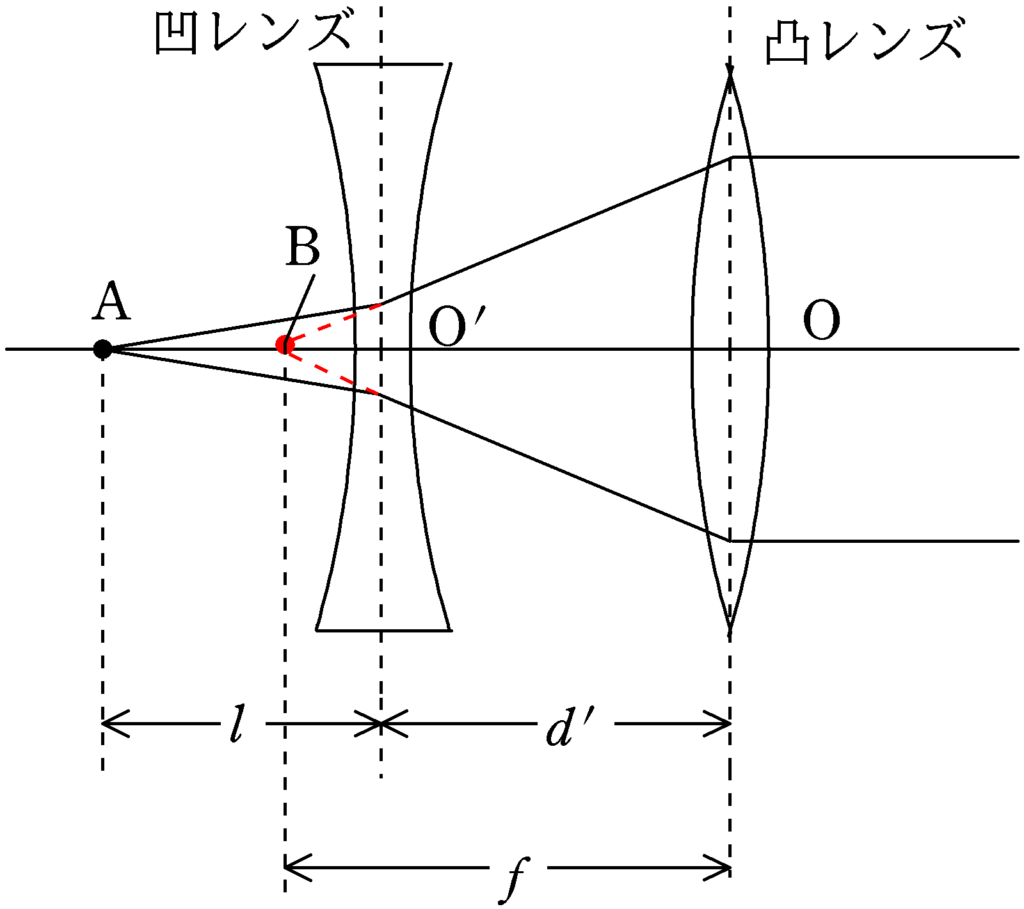
一方,Aから出た光が凹レンズで屈折した光はBから出てきたように曲げられているので,凹レンズにとって点Bは虚像となります.この後はレンズの式で計算してもいいですが,今回はレンズの式は使わずに相似を用いて$\rm BO’$を計算したいと思います.
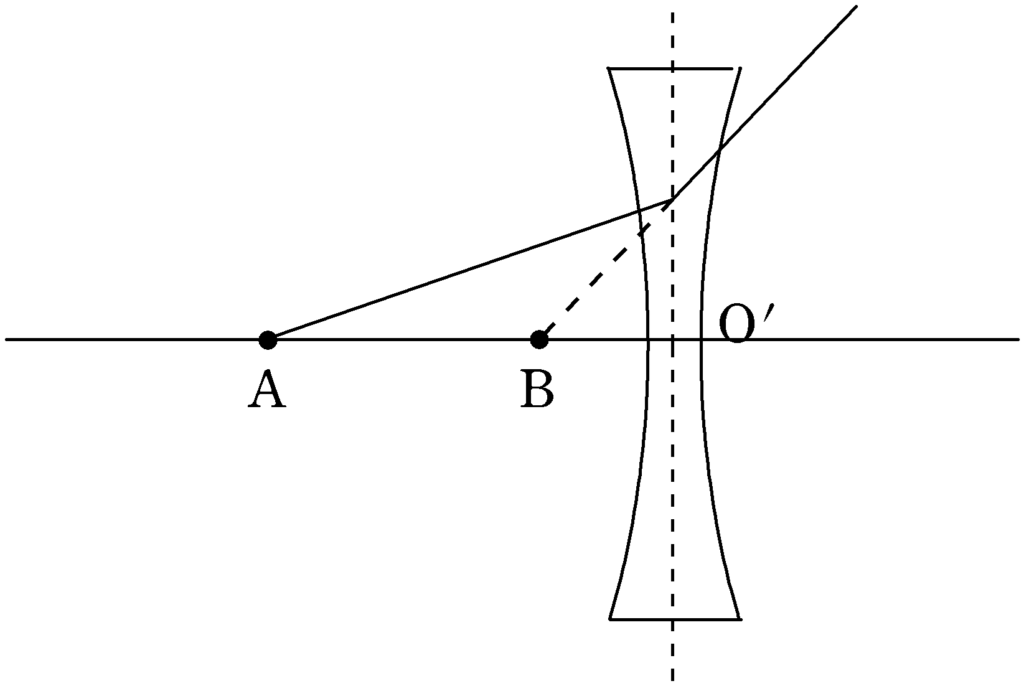
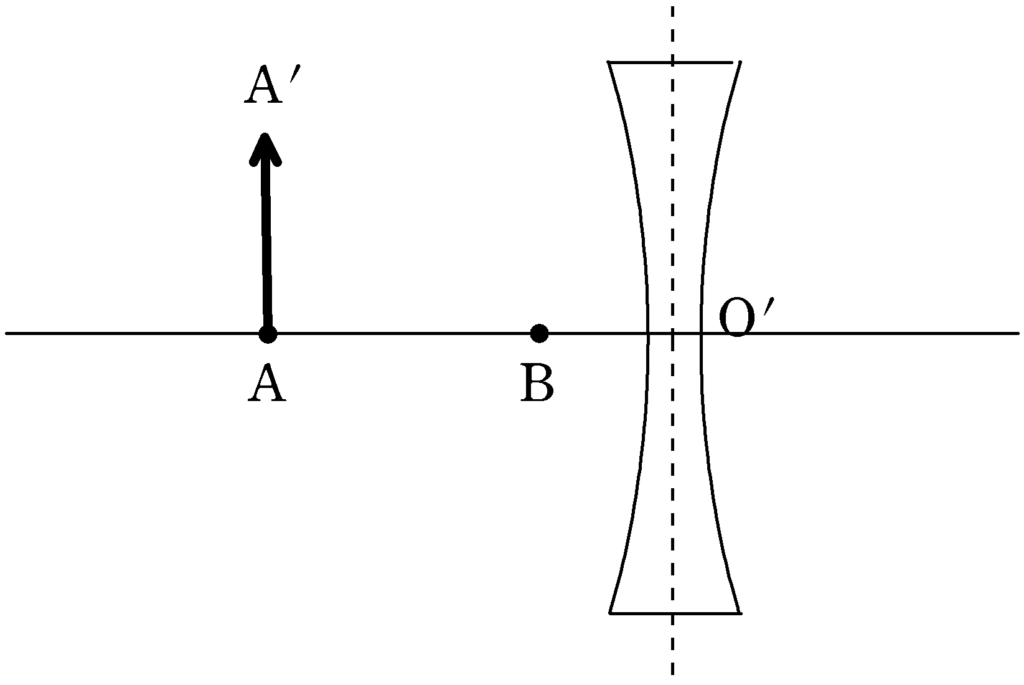
光軸上に光源があると,作図がしずらいので,下図のように光源を$\rm A’$にうつして考えます.すると,$\rm A’$を光源にしたときの虚像は$\rm B$を通り光軸に垂直な直線上のどこかにあるはずです.
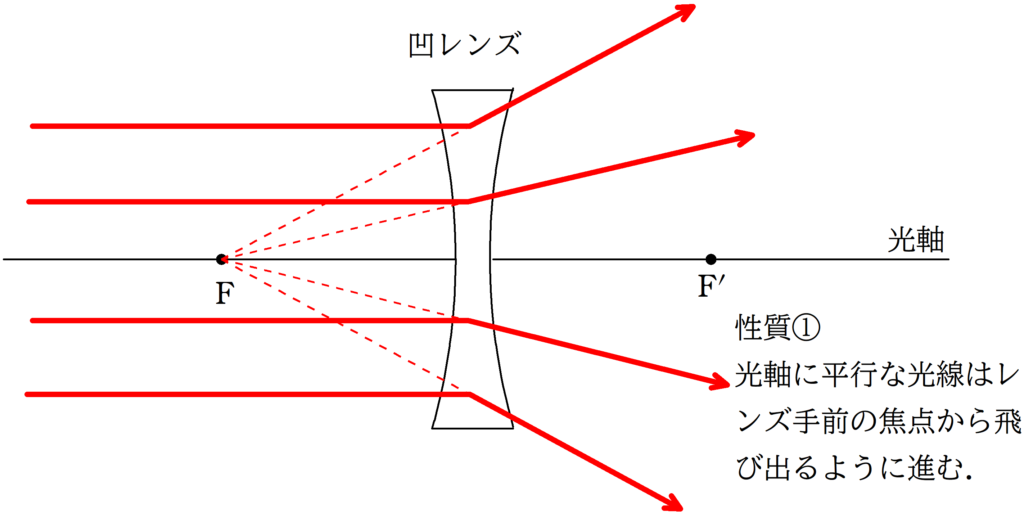
凹レンズの代表光線を確認しておきましょう.
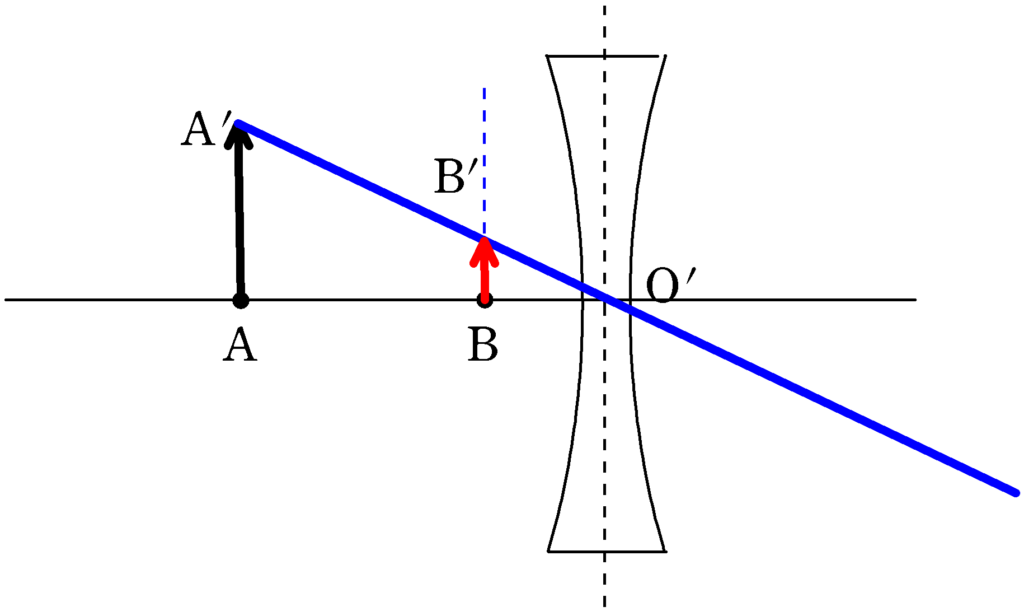
まずは性質②の「中心を通る光線はそのまままっすぐ進む」という性質から下図のように$\rm A’$が光源だった場合の虚像の位置$\rm B’$がわかります.
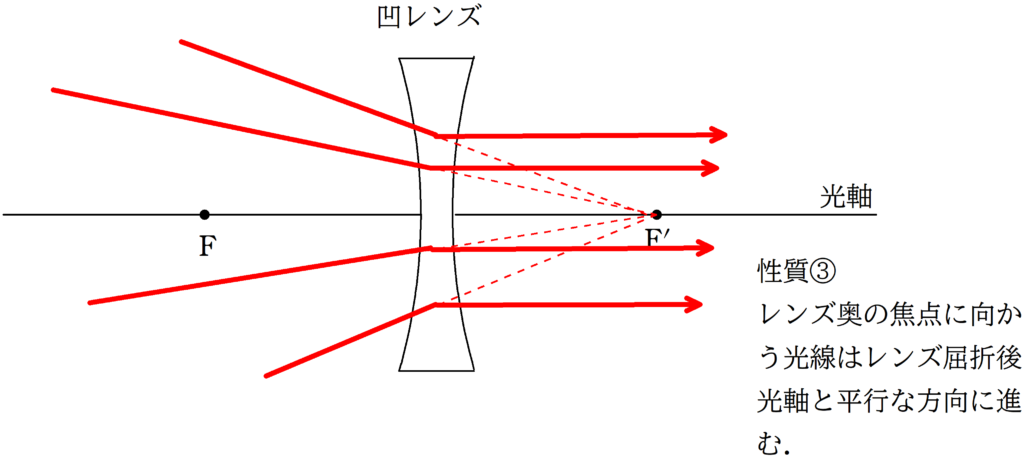
次に,性質①の「光軸に平行な光線はレンズ手前側の焦点から飛び出るように進む」ことから,凹レンズの焦点$\rm F’$がわかります.
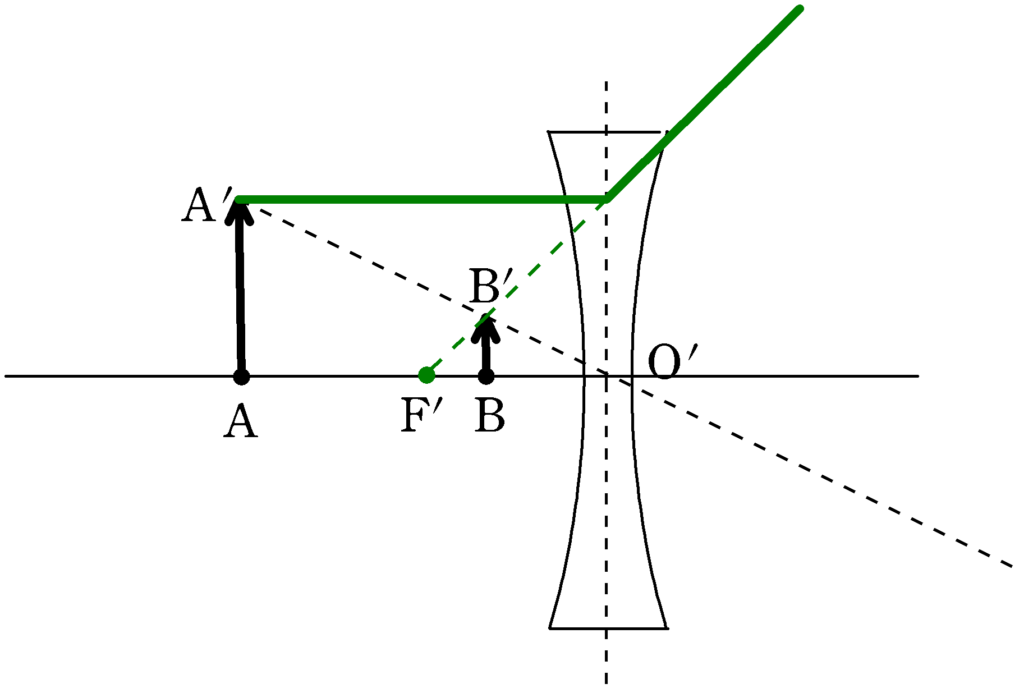
${\rm O’B=}b$,${\rm AA’}=X$,${\rm BB’}=Y$として,下図の2組の相似な三角形の相似比を考えることで$b$を計算したいと思います.
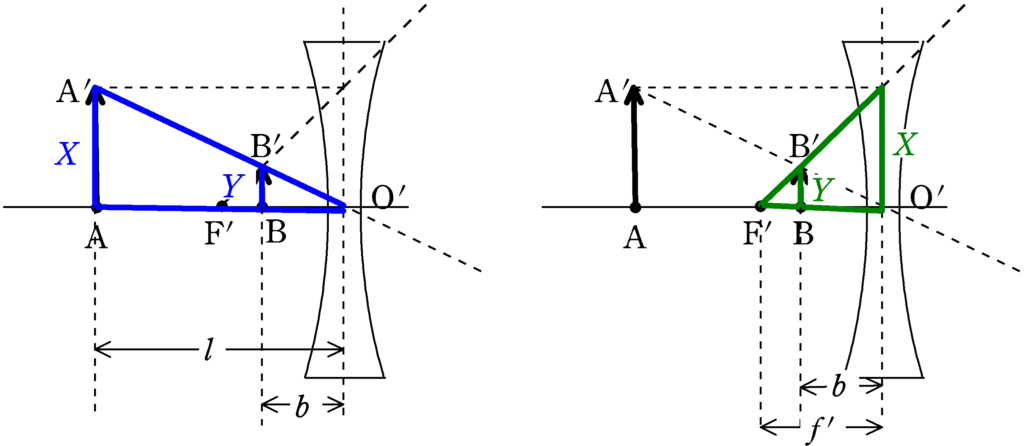
★ 青の三角形の相似
$\dfrac{Y}{X}=\dfrac{b}{l}$ $\cdots (\ast)$
★ 緑の三角形の相似
$\dfrac{Y}{X}=\dfrac{f’-b}{f’}$ $\cdots (2\ast)$
$(\ast),(2\ast)$より
$\dfrac{b}{l}=\dfrac{f’-b}{f’}$ $\therefore\,\, b=\dfrac{f’l}{l+f’}$
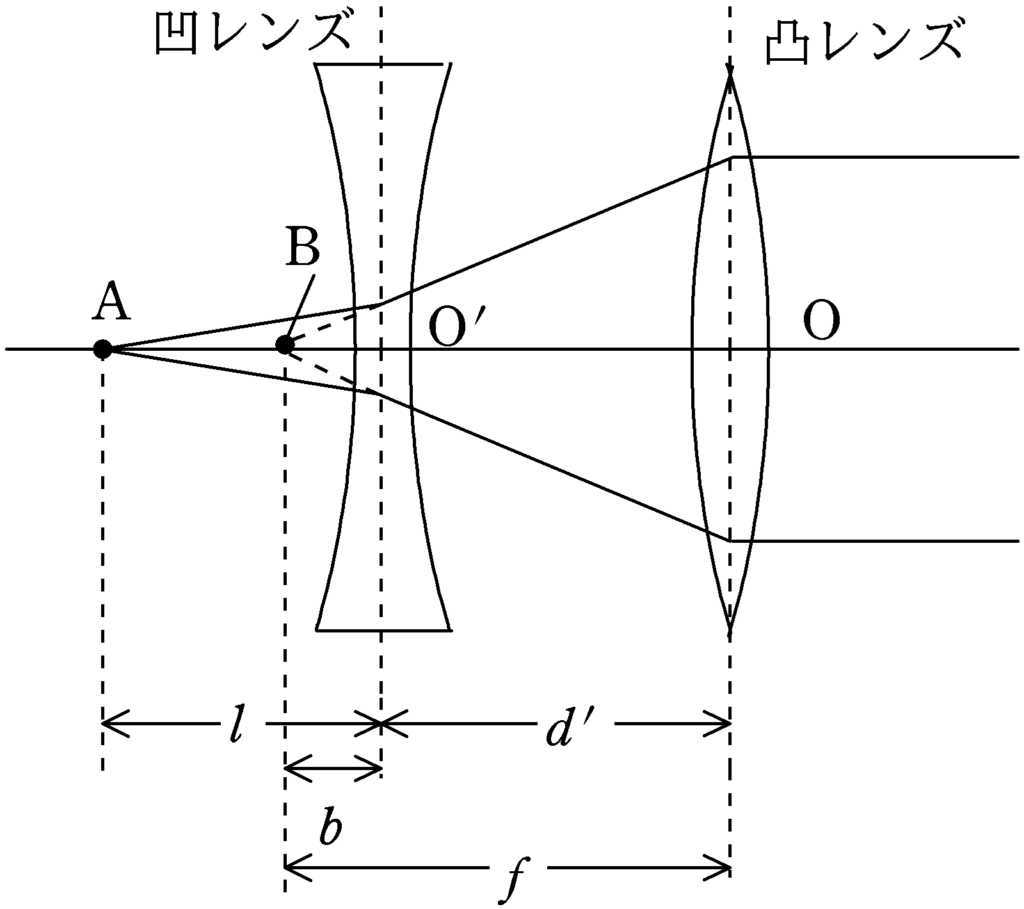
したがって,上図より
$d’=f-b=f-\dfrac{f’l}{l+f’}$ (答)
レンズや鏡の作図や式については下のリンク先にまとめてあります.




コメント