
線密度$\rho$,張力の大きさ$S$の弦を伝わる速さ$v$は
$v=\sqrt{\dfrac{S}{\rho }}$
っていうのは,覚えているんだけど,その証明の問題で,なぜか円運動の運動方程式を立てているんだよね.なんでなんだろう??

弦を伝わる速さの証明はいくつかありますが,正弦波が伝わるときの証明問題のことですね.
それでは,なぜ,円運動の運動方程式を立てるのか,順を追って説明していきたいと思います.
波は媒質の振動が遅れて伝わる現象

波動とは,媒質(振動するもの今回なら弦)の振動が遅れて伝わっていく現象のことを言います.
媒質が単振動しているときに正弦波ができます.
次の図をみて,媒質の振動が遅れて伝わる様子を確認してみてください.
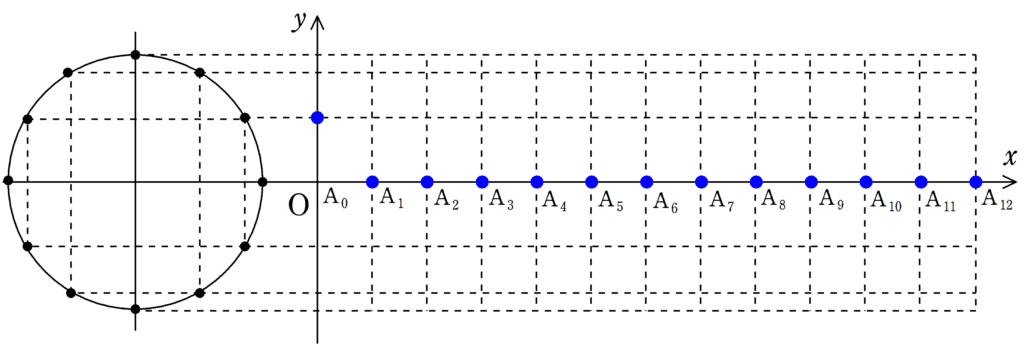
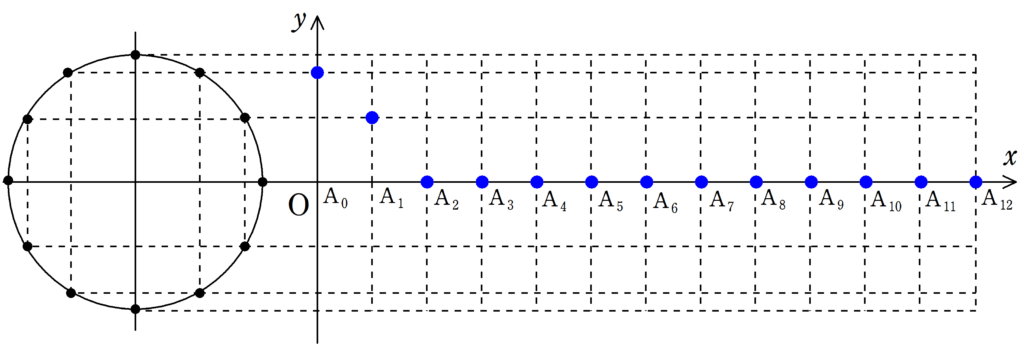
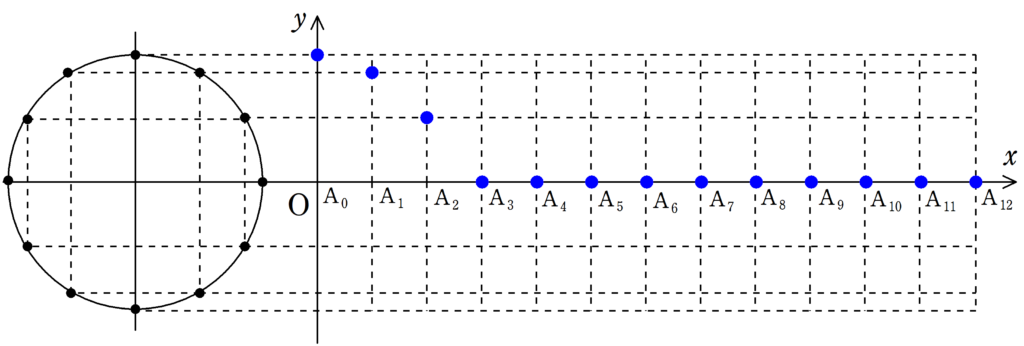
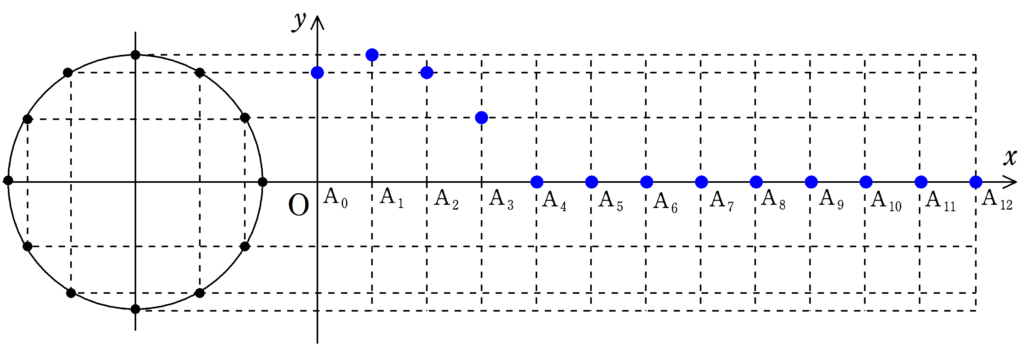
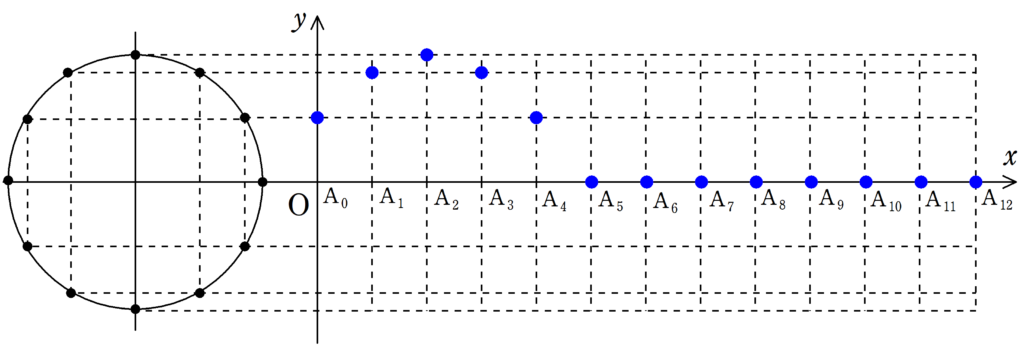
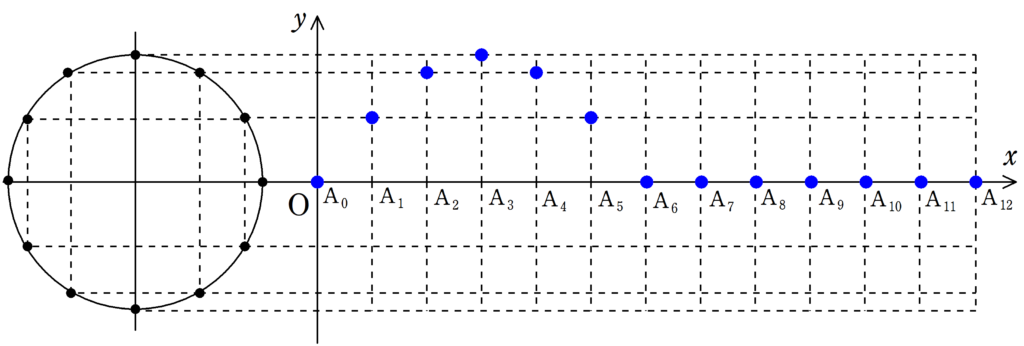
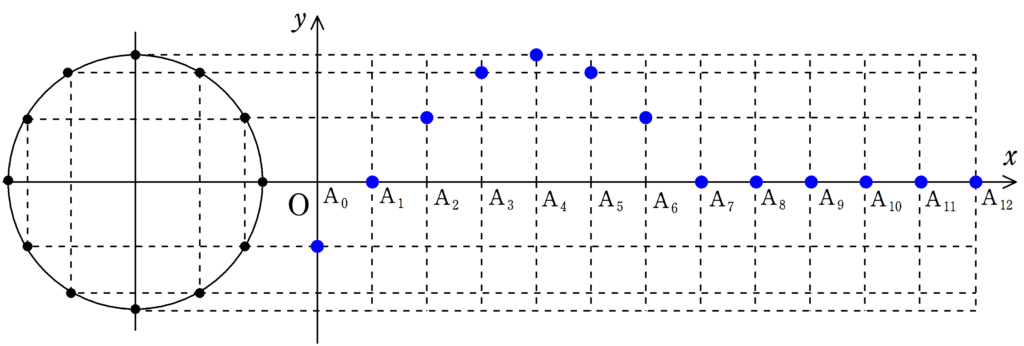
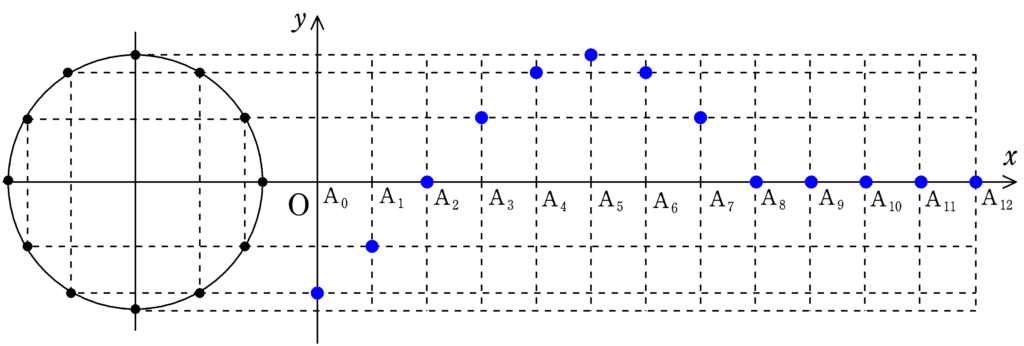
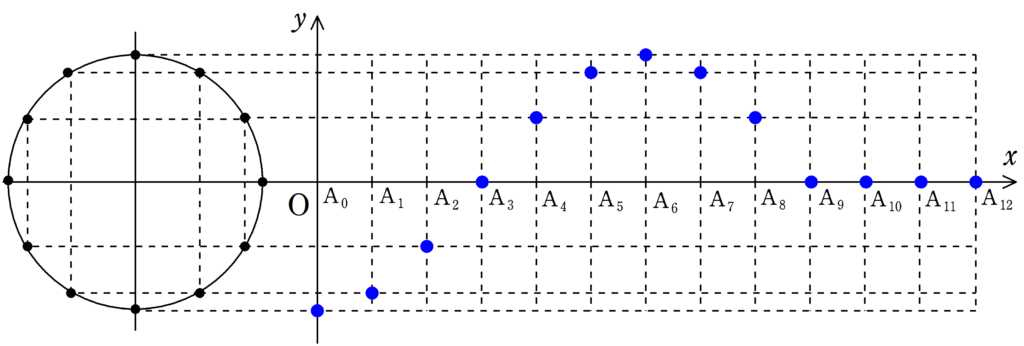
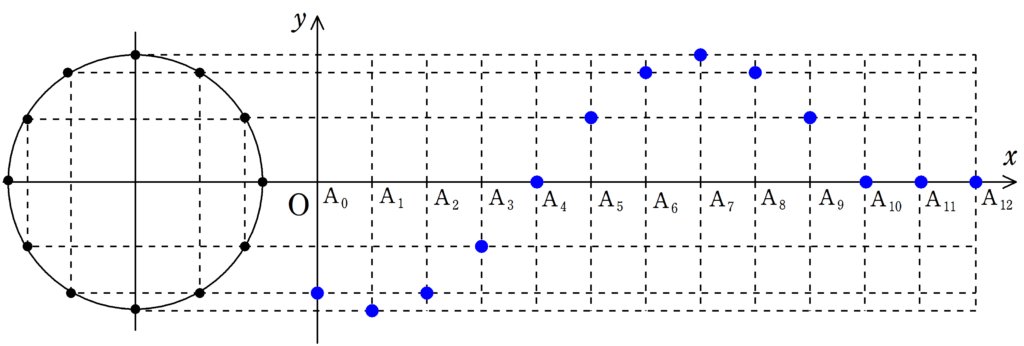
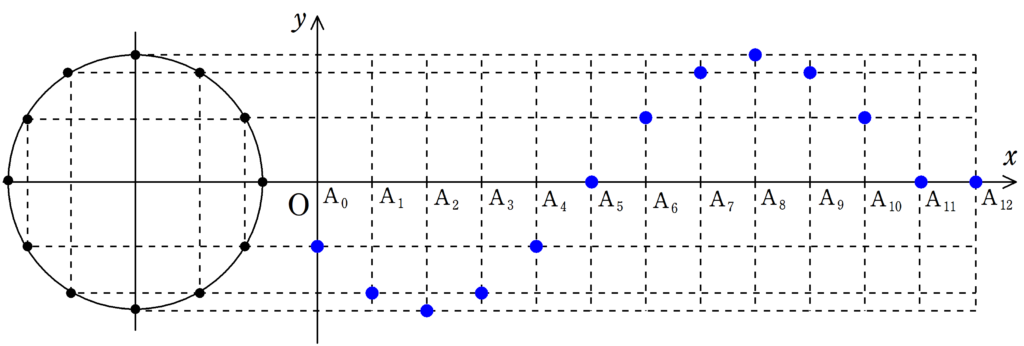
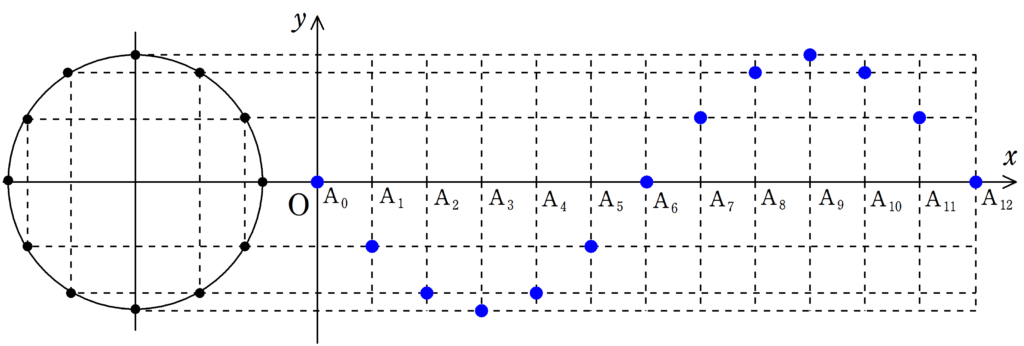

各媒質の振動が伝わることで波が作られている様子が確認できたと思います.
波の「山」の部分に着目すれば,波がどちらに移動しているか確認しやすいと思います.
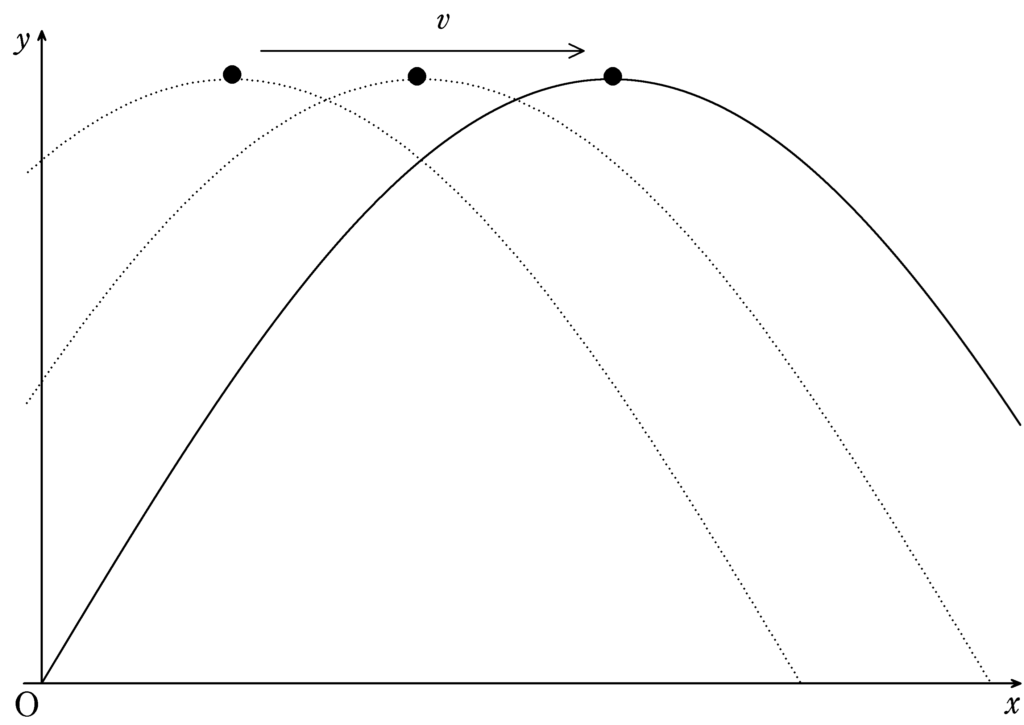

そこで,山付近の部分がどのくらいの速さで移動しているかを考えていきます.
下図のように,山付近は円の一部とみることができそうです.
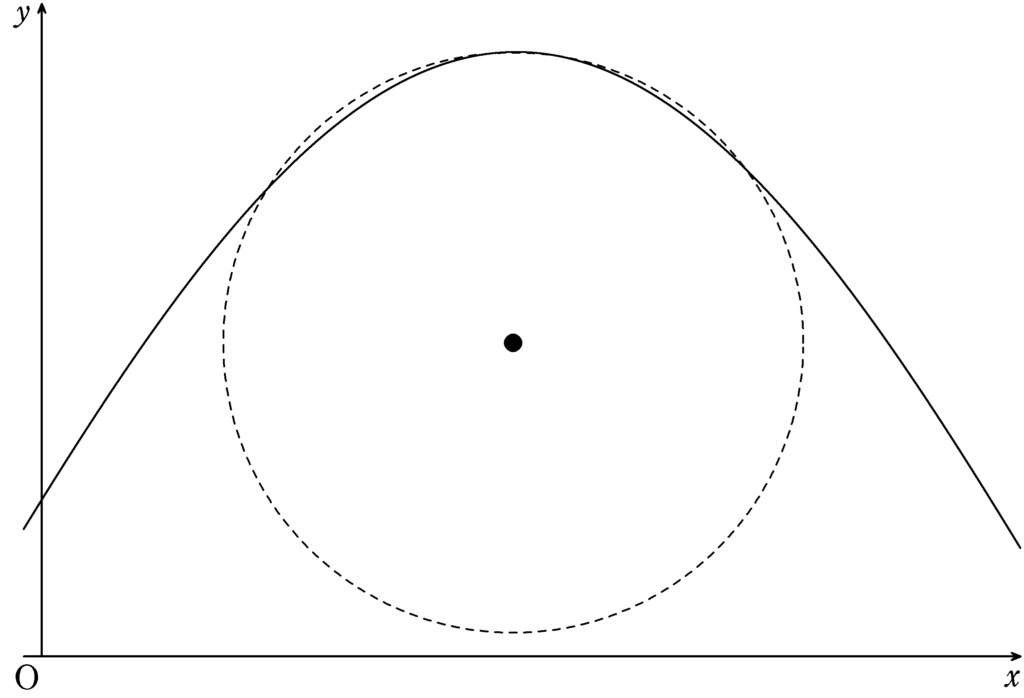
波の山と同じ速さで移動した観測者を考える.
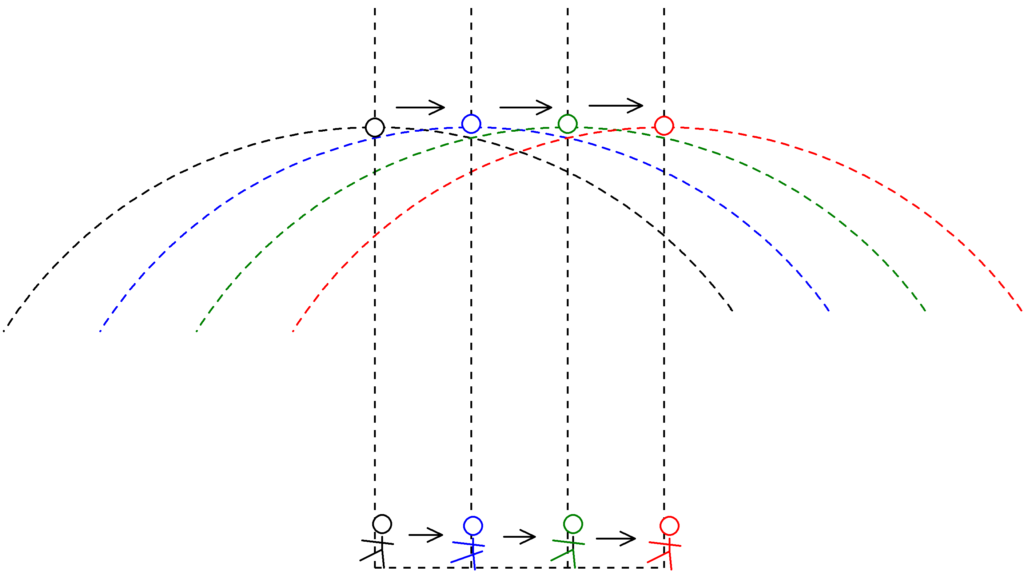

波が伝わる速さを計算するにあたって,波の「山」の部分と同じ速さで移動している観測者からみていきたいと思います.
上図は,はじめ黒色で書かれた観測者が時間が経つごとに,山(上図白丸)とともに青色で書かれた観測者,緑色で書かれた観測者,赤色で書かれた観測者と移動している様子を書いています.
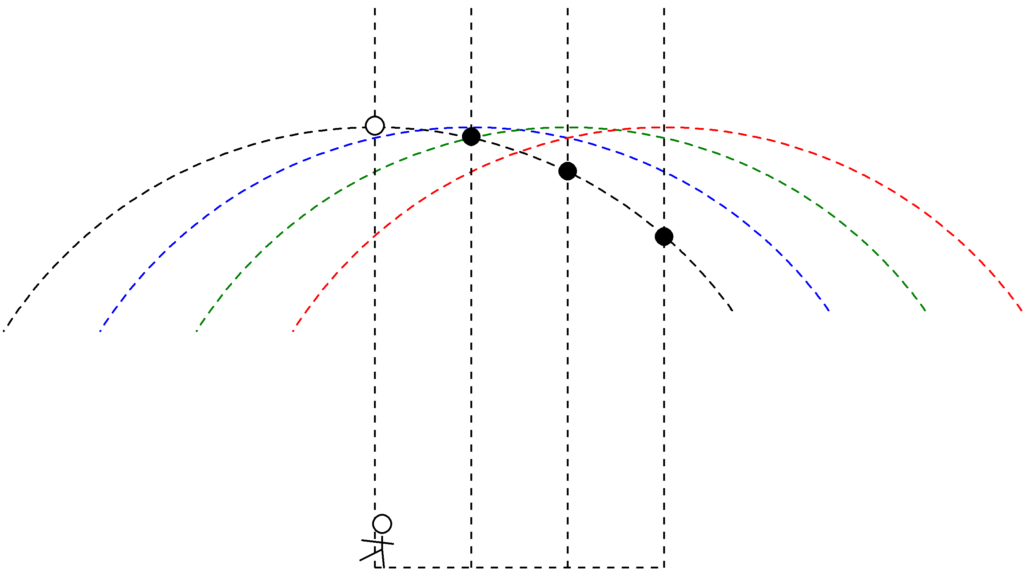

ここから,ある時間ごとに写真をとった様子を見ていきたいと思います.
はじめ,観測者が左端にいて,そのすぐ上に山(白丸)があります.山より低いところにある媒質は黒色で書かれています.
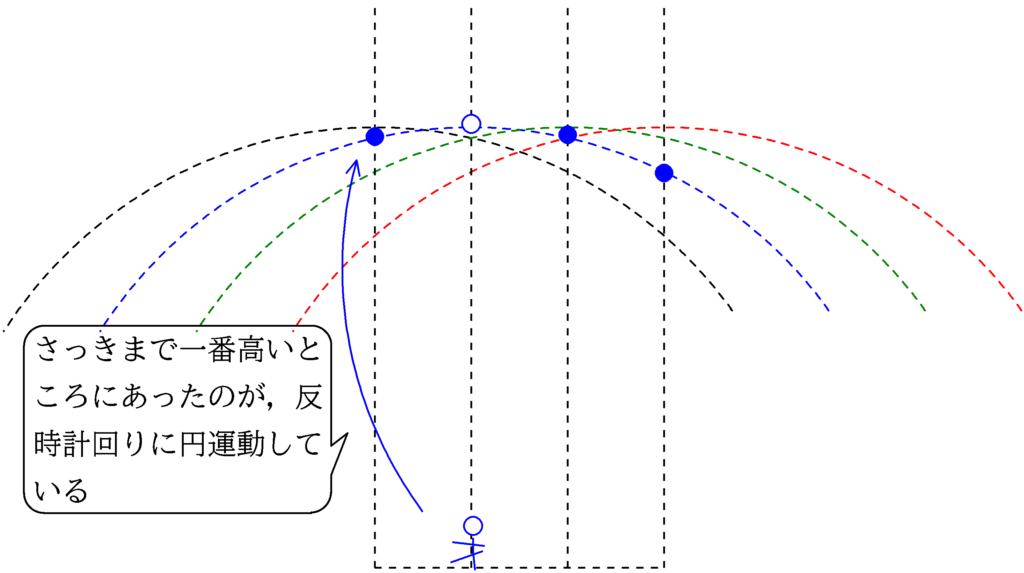

山が移動すると,観測者も移動します.すると,一番左端の列にあった媒質が下に落ちてきて,「山」とともに移動している観測者からみると,反時計回りに円運動しているようにみえます.
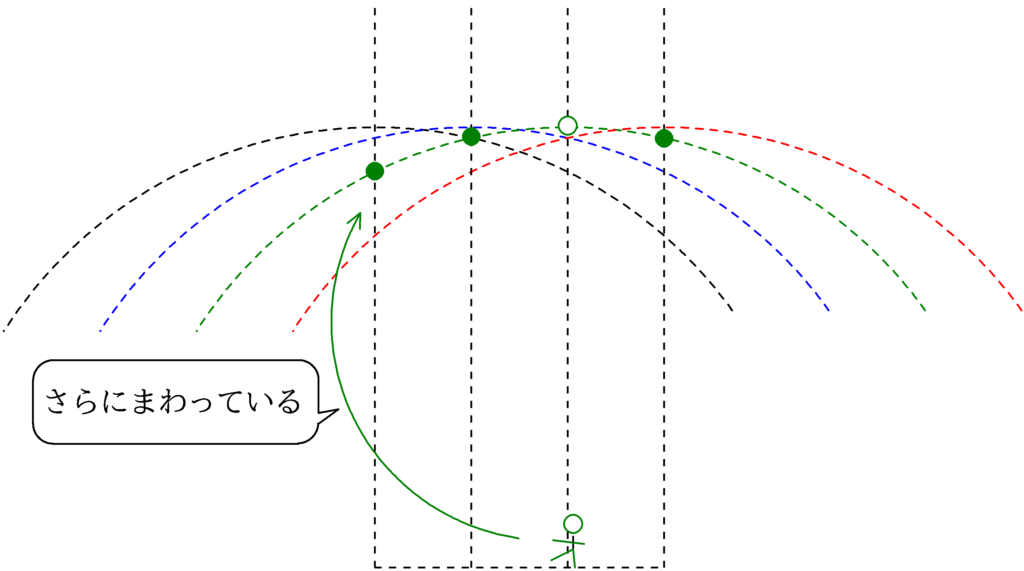
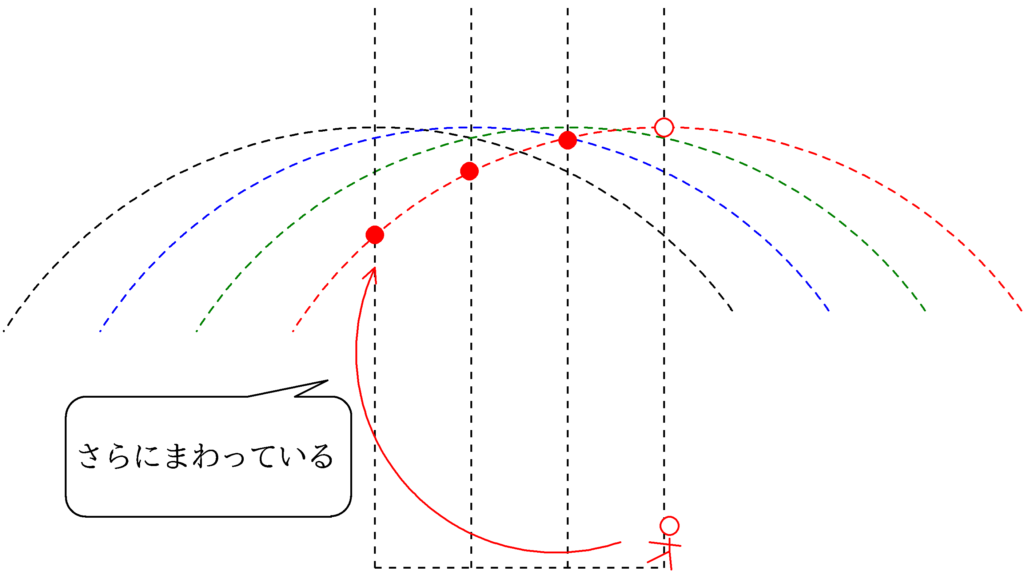

上図のように,観測者が移動するとさらに反時計回りに円運動しているようにみます.(近似的に)
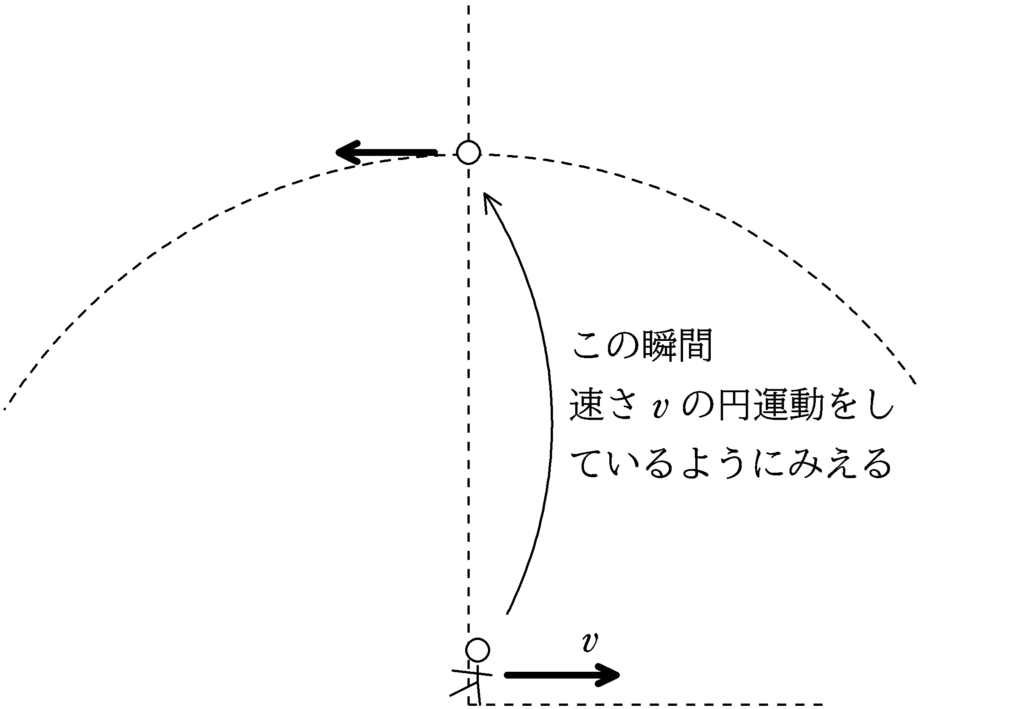

つまり,「山」とともに速さ$v$で移動する観測者からみると,「山」の部分にある媒質が接線方向の速さ$v$の円運動をしているように見えるわけか.
円運動の接線方向の速さは円運動の向心加速度と関係があったね.
だから,向心方向の運動方程式を立てて,速さ$v$を求めるのか.
半径$r$,円運動の接線方向の速さを$v$,角速度を$\omega$とすると,向心加速度の大きさ$a$は
$a=\dfrac{v^{2}}{r}=r\omega^{2}$
向心加速度の向きは円運動の中心
向心方向の運動方程式を立てて速さ$v$を求める.
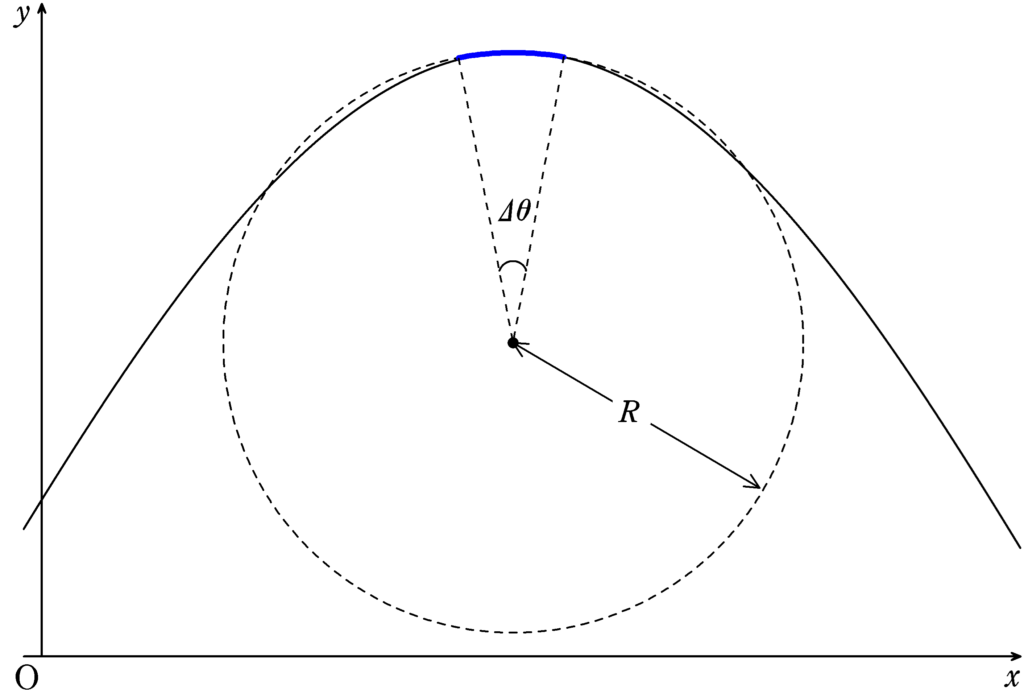

それでは,上図のように,山付近の部分(青色部分)にはたらく向心力を求めて,向心方向の運動方程式を立てていきたいと思います.
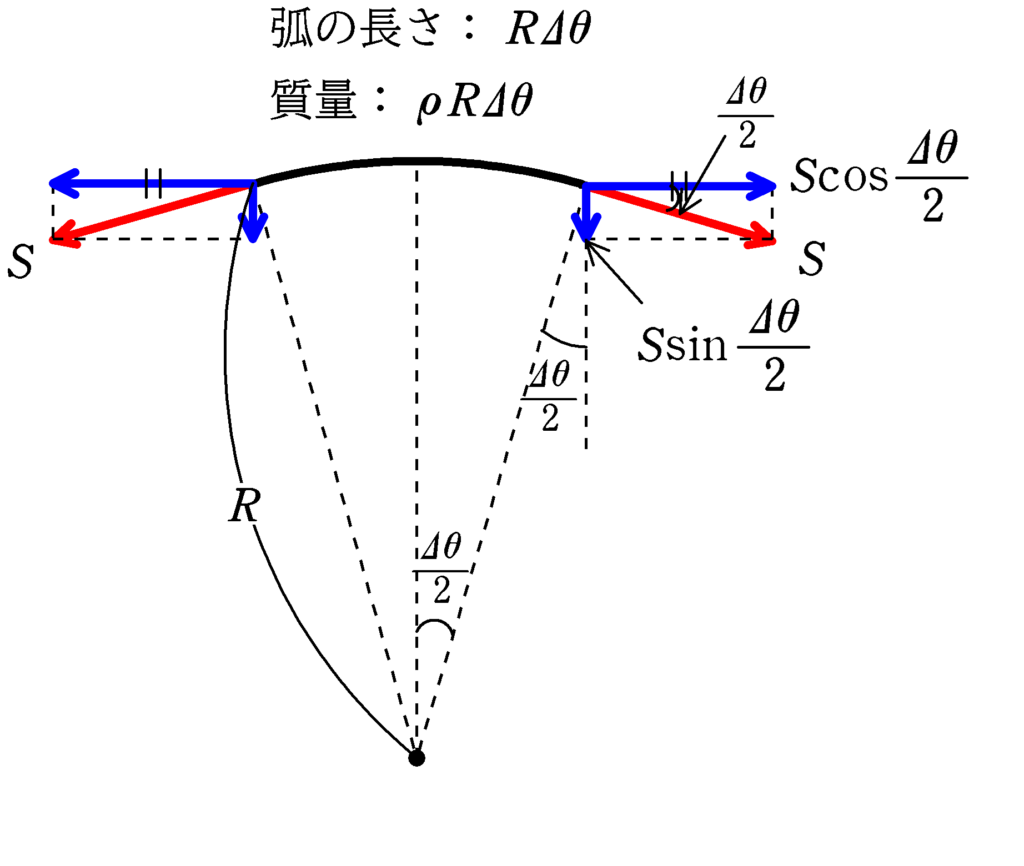
半径$R$の円の一部と考え,そのうちの角度$\varDelta \theta$の弧について考えます.$\varDelta \theta$は弧度法で表された角度です.
弧の長さは
$2\pi R\times \dfrac{\varDelta \theta}{2\pi}=R\varDelta \theta$
なので,線密度を(単位長さあたりの質量)$\rho$とすれば,弧の部分の質量は
$\rho R\varDelta \theta$
となります.
また,張力の大きさを$S$として,弧の部分は下図のように赤色矢印の方向に引っ張られます.
これを横と縦に分解すると,横の部分は同じ大きさ$S\cos\dfrac{\varDelta \theta}{2}$で逆向きの力なので打ち消し,縦部分の$S\sin\dfrac{\varDelta \theta}{2}$の合力が向心力となります.$\theta$が非常に小さいとき
$\sin\theta\fallingdotseq \theta$を利用すると,弧の部分の向心力の大きさは
$2\times S\sin\dfrac{\varDelta \theta}{2}\fallingdotseq 2S\cdot \dfrac{\varDelta \theta}{2}=S\varDelta \theta $
となります.
★ 向心方向の運動方程式
$\eqalign{\rho \cancel{R}\bcancel{\varDelta \theta}\times \dfrac{v^{2}}{\cancel{R}}&=S\bcancel{\varDelta \theta}\\ \therefore\,\, v^{2}&=\dfrac{S}{\rho }\\ \therefore\,\, v&=\sqrt{\dfrac{S}{\rho }}}$

これで,$v=\sqrt{\dfrac{S}{\rho}}$が導けたね.



コメント