
前回は凹レンズを通過する光線の作図の問題を扱いました.
今回は,凹レンズの式についてです.
そして,最後に凸レンズと凹レンズのレンズの式をまとめていきたいと思います.
前回の内容はこちら.

覚えておいて欲しい代表光線は次の3つです!
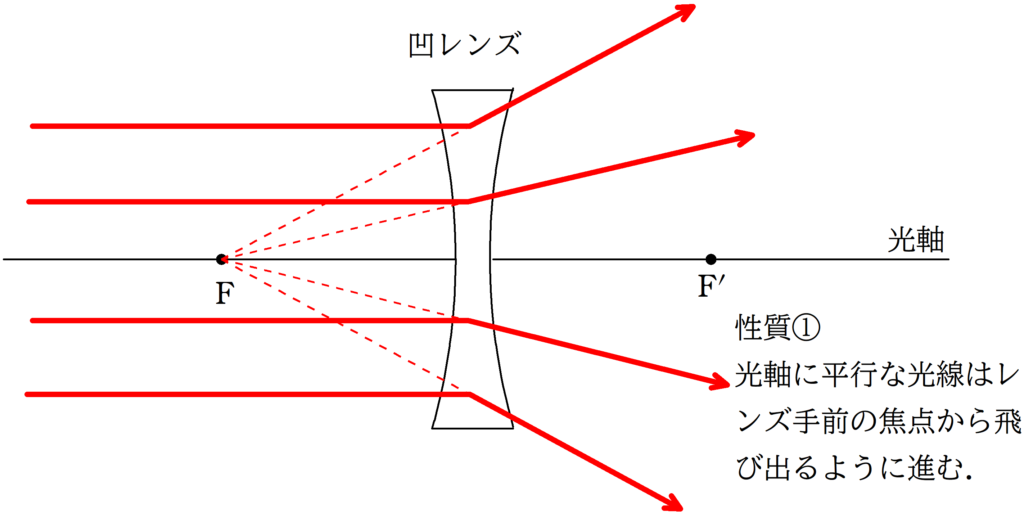
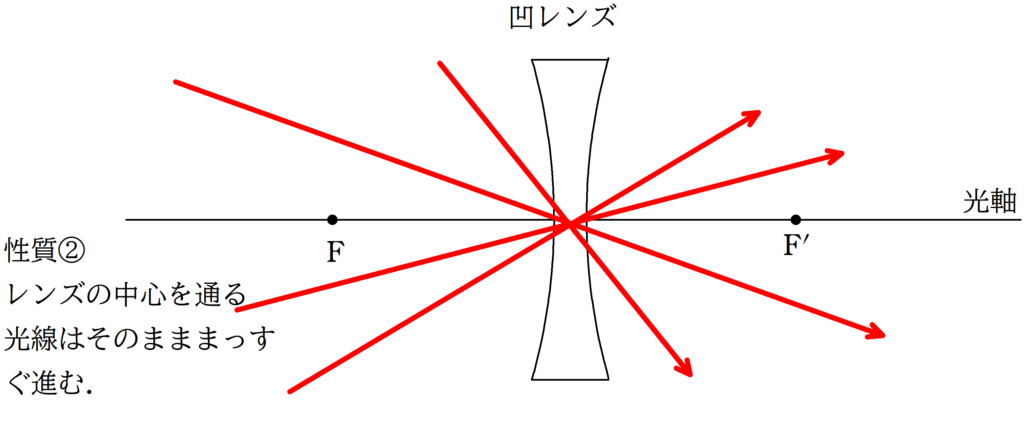
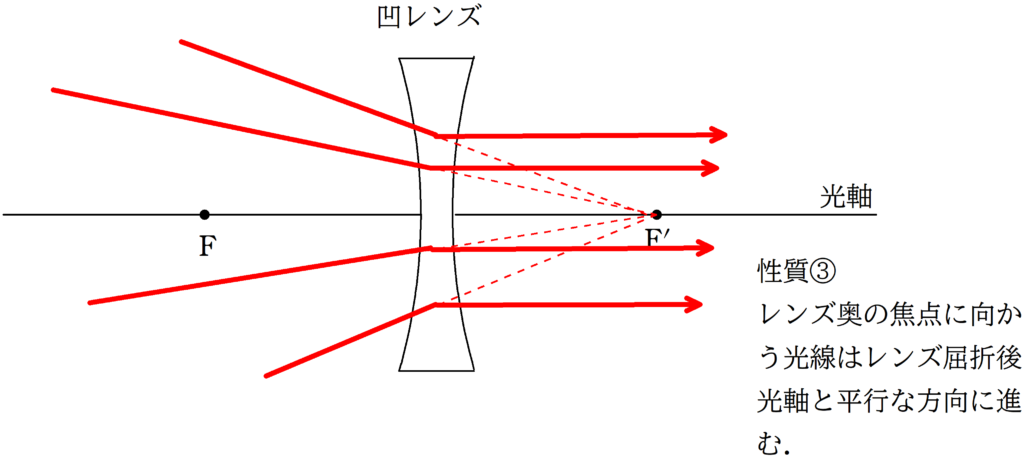
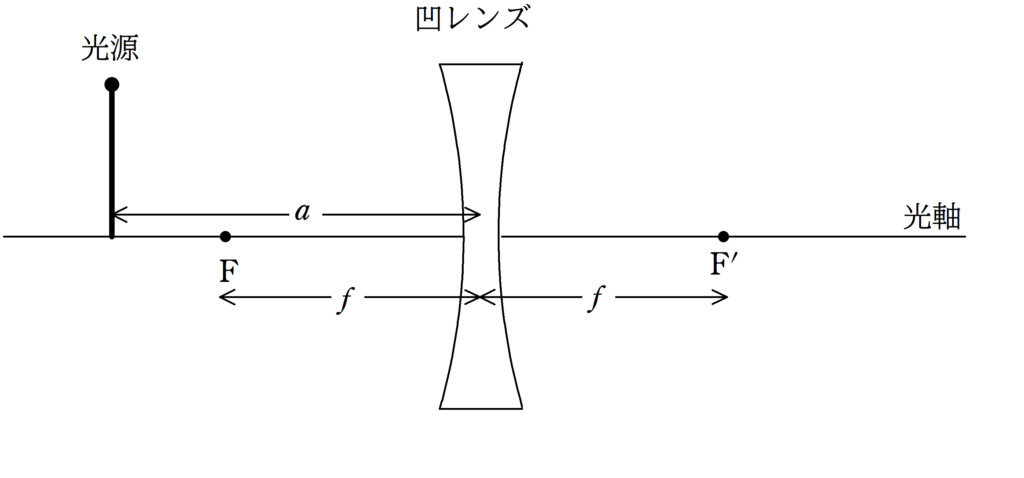
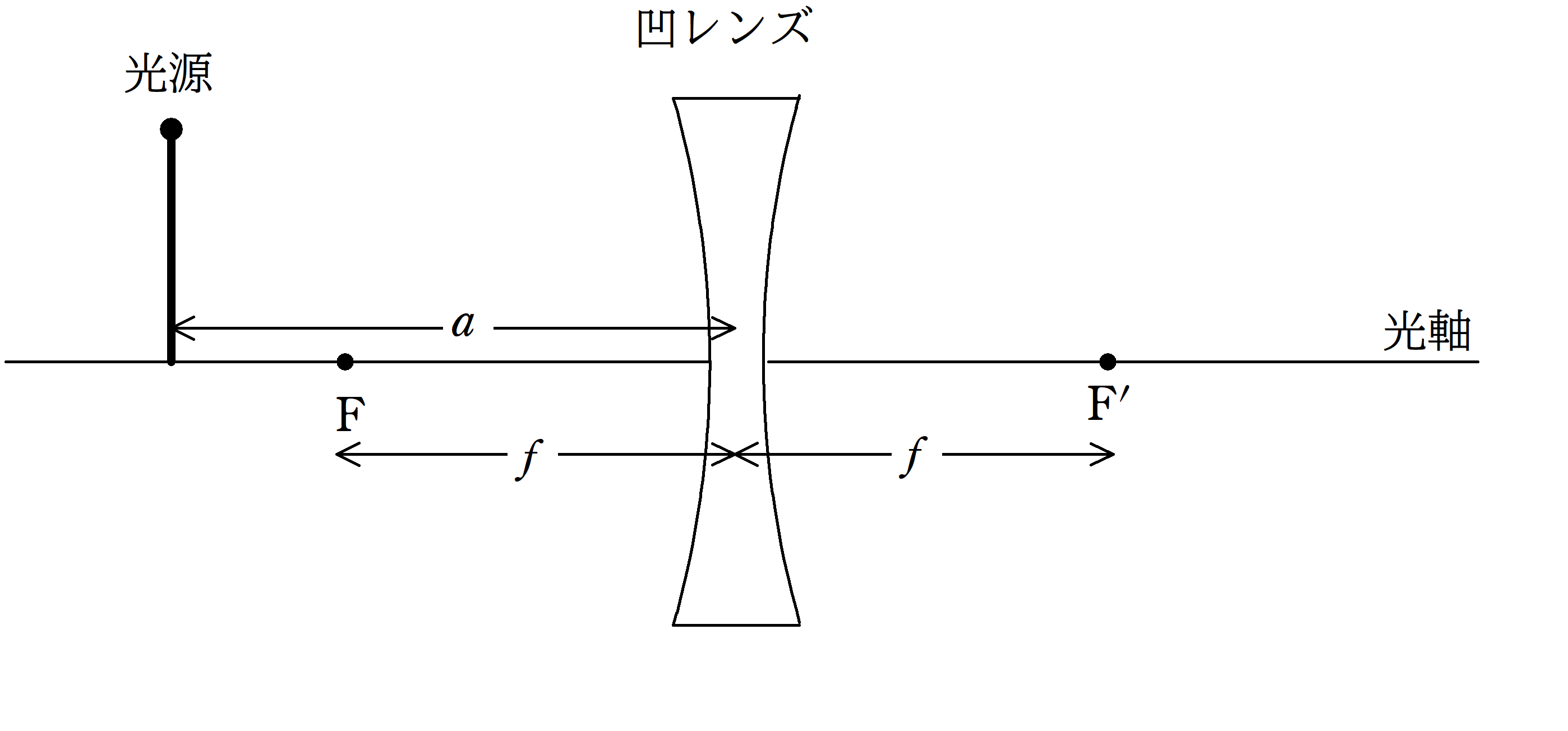
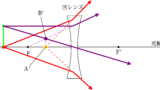
上図のように,焦点を$\rm F$,$\rm F^{\prime}$とする凹レンズがおかれている.
焦点距離$f$の凹レンズから距離$a$の場所に光源をおくと,虚像ができた.
この虚像と凹レンズとの距離を$b$とする.
このとき,$a$,$b$,$f$の関係式を導け.
<解答>

まずは,代表光線をかいてみましょう.
その結果,光線はレンズ通過後に発散するので,反対側に線を伸ばして,虚像の位置を確認します.
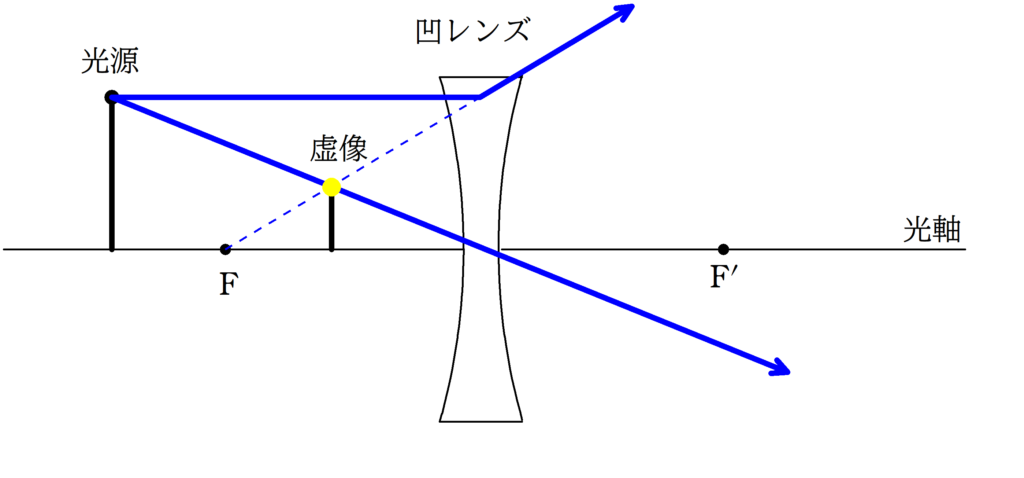

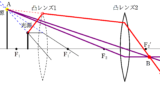
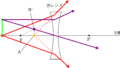
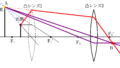
次に,光源の高さを$X$,虚像の高さを$Y$として,$X$と$Y$を含む2組の相似な図形について考えましょう.
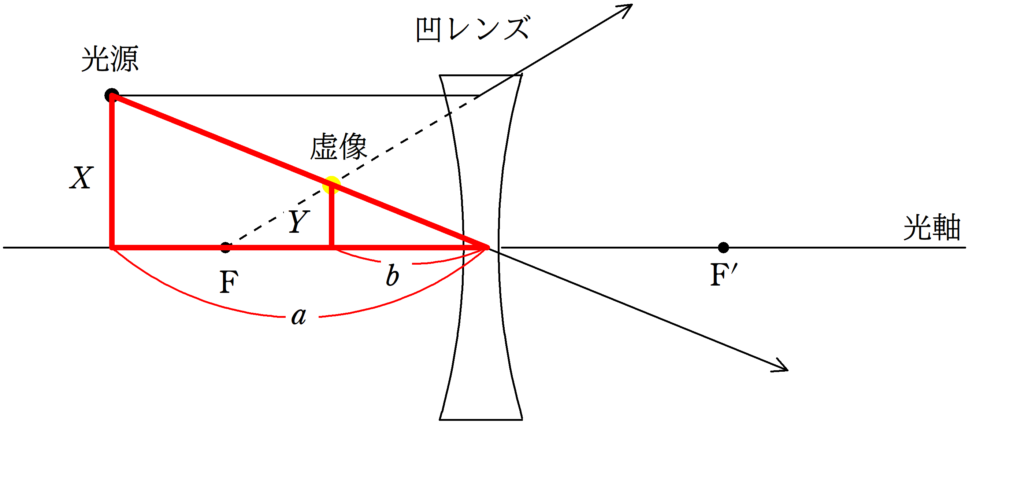
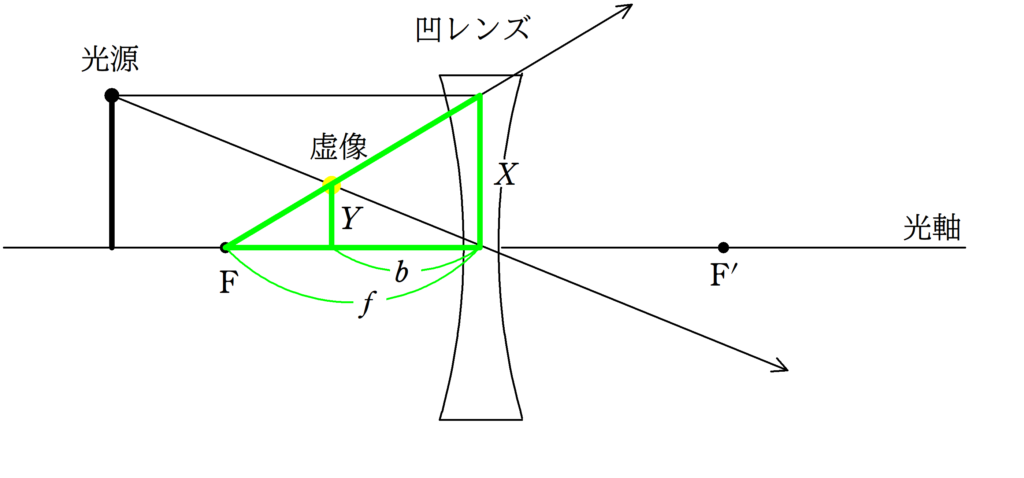

すると,上のような赤の相似な図形と緑の相似な図形が見つかるね.
相似比をかいてみると次のようになります.
$\dfrac{Y}{X}=\dfrac{b}{a}$ $\dots (\ast)$
$\dfrac{Y}{X}=\dfrac{f-b}{f}$ $\dots (2\ast)$
$(\ast)$,$(2\ast)$より
$\eqalign{\dfrac{b}{a}&=\dfrac{f-b}{f}\cr bf&=a(f-b)\cr bf-af&=-bf}$
両辺$abf$で割って
$\dfrac{1}{a}-\dfrac{1}{b}=-\dfrac{1}{f}$ (答え)

凸レンズも含めてレンズの式を書き出すと次のようになります.
レンズと光源との距離を$a$,レンズの焦点距離を$f$,レンズと像までの距離を$b$とする.
★ 凸レンズ 実像ができるとき
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}$
★ 凸レンズ 虚像ができるとき
$\dfrac{1}{a}-\dfrac{1}{b}=\dfrac{1}{f}$
→ $\dfrac{1}{a}+\dfrac{1}{(-b)}=\dfrac{1}{f}$
★ 凹レンズ 虚像ができる(単体では実像はできない)
$\dfrac{1}{a}-\dfrac{1}{b}=-\dfrac{1}{f}$
→ $\dfrac{1}{a}+\dfrac{1}{(-b)}=\dfrac{1}{(-f)}$

なんでわざわざマイナスを括弧の中にいれて変形したの?

式を統一するためです.
レンズの式は次のようにまとめることができます.
レンズと光源との距離を$|a|$,焦点距離を$|f|$,レンズと像との距離を$|b|$とする.
このとき,次の式が成り立つ.
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}$
ただし,次の規則で$b$と$f$の正負を決める.
$b>0 \dots$ 実像, $b<0 \dots$ 虚像
$f>0 \dots$ , 凸レンズ $f<0 \dots$ 凹レンズ

具体的な問題を解いてみたいな.

それでは,いくつか問題を解いてみましょう.
次の問題を解きなさい.
(1) 凸レンズと光源の距離を$30\rm cm$,焦点距離が$15\rm cm$のとき,できる像は実像か虚像か?また,その像とレンズとの距離を求めなさい.
(2) 凹レンズと光源の距離を$15\rm cm$,焦点距離が$30\rm cm$のとき,できる像は実像か虚像か?また,その像とレンズとの距離を求めなさい.
<解答>
(1) 凸レンズなので,$f>0$とする.レンズの式より
$\dfrac{1}{30}+\dfrac{1}{b}=\dfrac{1}{15}$
$\therefore b=30$
$b>0$より,実像ができ,レンズとの距離は$\rm 30cm$
(2) 凹レンズなので,$f<0$とする.レンズの式より
$\dfrac{1}{15}+\dfrac{1}{b}=\dfrac{1}{(-30)}$
$\therefore b=-10$
$b<0$なので,虚像ができ,レンズとの距離は$\rm 10cm$

次回の内容はこちらです.

コメント
[…] レンズの演習問題⑥ レンズの式(凹レンズ)+まとめPHYさん前回は凹レン… […]
[…] レンズの演習問題④ 凹レンズの作図① レンズの演習問題⑥ レンズの式(凹レンズ)+まとめ […]