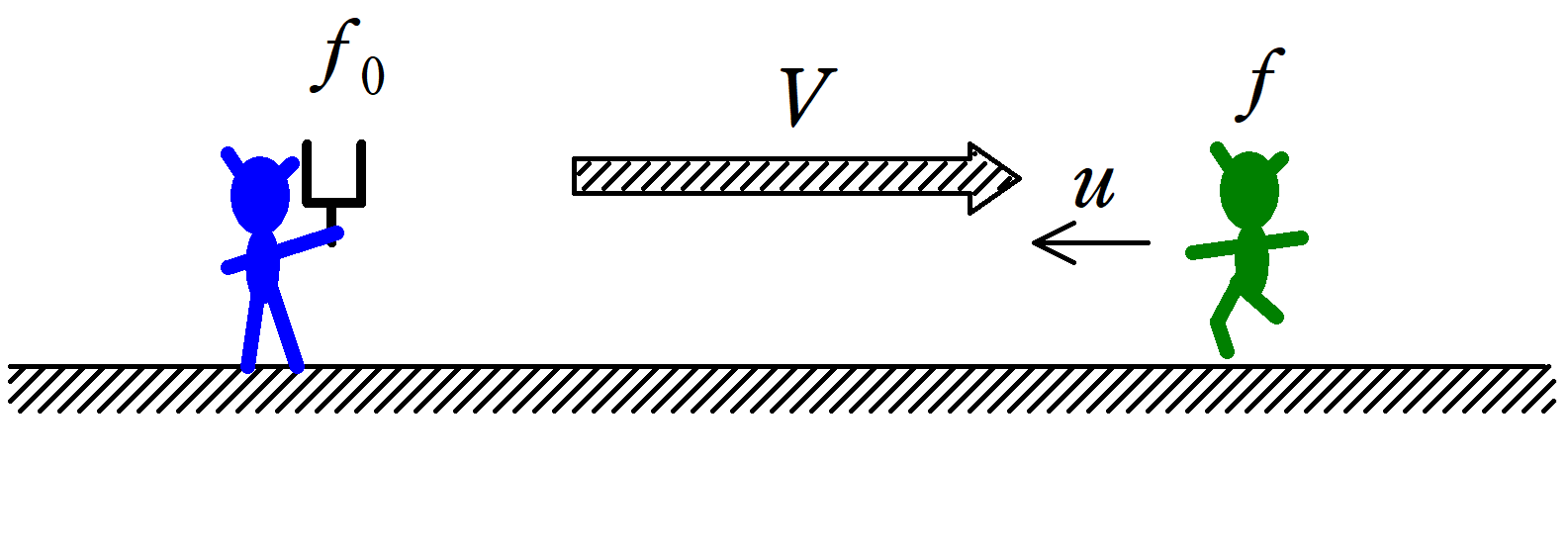
振動数$f_{0}[\rm Hz]$の音源をもった青の人と,観測者である緑の人がいる.
一直線上の運動のみを考えるとき,次の各々の場合について,緑の人(観測者)の観測する振動数$f[\rm Hz]$を求めよ.
ただし,音速は$V[\rm m/s]$で一定であり,風は吹いていないものとする.
(1) 音源をもった青の人が右方向に速さ$v[\rm m/s]$で動き,観測者である緑の人が静止しているとき.

(2) 音源をもった青の人が静止していて,観測者である緑の人が左方向に速さ$u[\rm m/s]$で動いているとき.
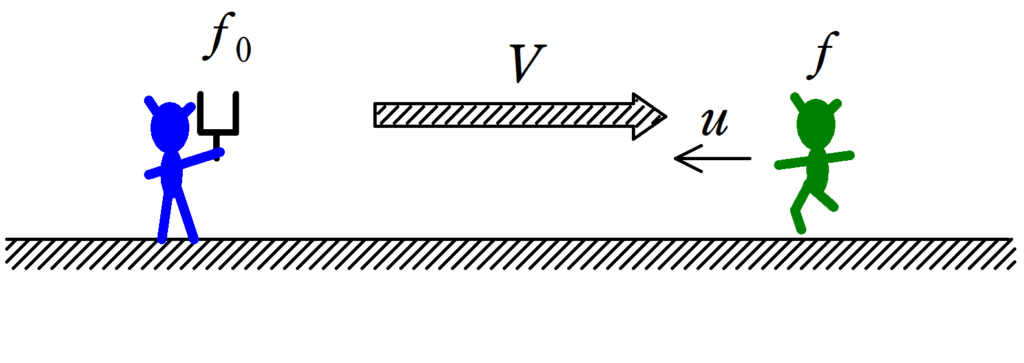
(3) 音源をもった青の人が右方向に速さ$v[\rm m/s]$で動き,観測者である緑の人が右方向に速さ$u[\rm m/s]$で動くとき.
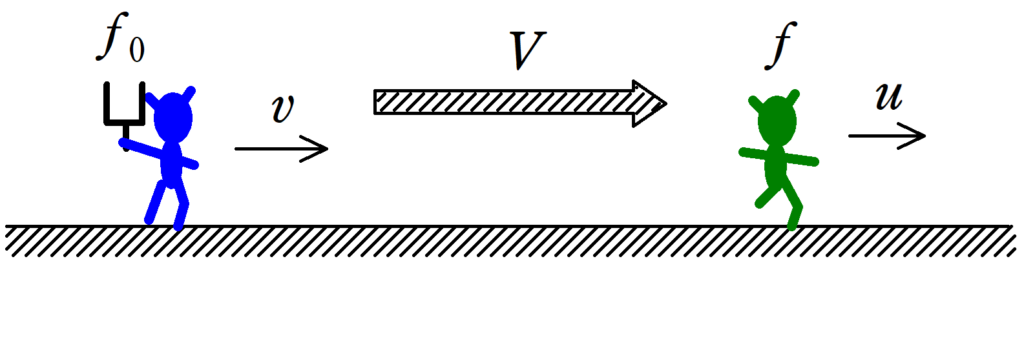
(4) 音源をもった青の人が左方向に速さ$v[\rm m/s]$で動き,観測者である緑の人が右方向に速さ$u[\rm m/s]$で動くとき.
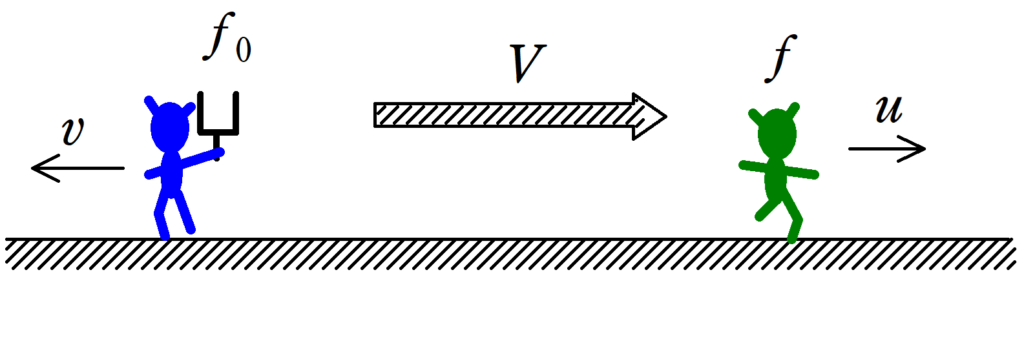
(5) 音源をもった青の人が右方向に速さ$v[\rm m/s]$で動き,観測者である緑の人が左方向に速さ$u[\rm m/s]$で動くとき.
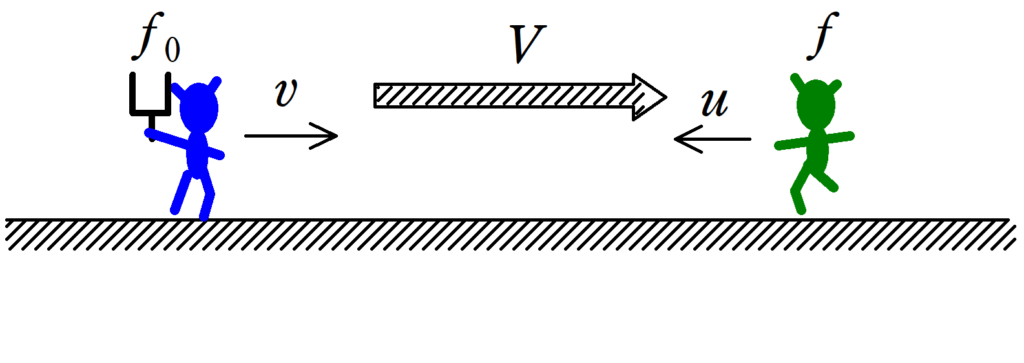

ドップラー効果の問題は次のことを確認してから解きましょう.
観測者が観測する振動数$f[\rm Hz]$は「$1 \rm s$間で観測者が受け取る波の数」を意味する.
波の数は次のように表すことができる.
波の波長を$\lambda$(波1個分の長さ),波の個数を$N$,波全体の長さを$\Delta L$とすると,次の関係式が成り立つ.
$\Delta L=N\cdot \lambda$
$\therefore N=\dfrac{\Delta L}{\lambda}$
このことから,
$f=\dfrac{1{\rm s}で受け取る波の長さ }{波の波長}$
で観測者が観測する振動数を求める.
以下,音源の振動数を$f_{0}$,音速を$V[\rm m/s]$,音源の速さを$v[\rm m/s]$,観測者の速さを$u[\rm m/s]$とする.
★ $1\rm s$で受けとる波の長さ
① 観測者が動かないとき→ $V\cdot 1$
② 観測者が音源に向かっているとき→ $(V+u)\cdot 1$
③ 観測者が音源から遠ざかっているとき→ $(V-u)\cdot 1$
★ 波の波長
① 音源が動かないとき→ $\dfrac{V}{f_{0}}$
② 音源の進行方向の波長→ $\dfrac{V-v}{f_{0}}$
① 音源の進行方向と逆の波長→ $\dfrac{V+v}{f_{0}}$
(1)


音源の前方の波長$\lambda^{\prime}$は
$\lambda^{\prime}=\dfrac{V-v}{f_{0}}$
に縮まっていますね.
また,観測者が$1\rm s$に受け取る波の長さ$L$は
$L=V\cdot 1$
以上より,観測者が観測する振動数$f$は
$\eqalign{f&=\dfrac{L}{\lambda^{\prime}}\\&=\dfrac{V}{\dfrac{V-v}{f_{0}}}\\&=\dfrac{V}{V-v}f_{0}[\rm Hz]}$ (答)
(2)


音源の前方の波長$\lambda^{\prime}$は
$\lambda^{\prime}=\dfrac{V}{f_{0}}$
で変化していません.
また,観測者が$1\rm s$に受け取る波の長さ$L$は
$L=(V+u)\cdot 1$
以上より,観測者が観測する振動数$f$は
$\eqalign{f&=\dfrac{L}{\lambda^{\prime}}\\&=\dfrac{V+u}{\dfrac{V}{f_{0}}}\\&=\dfrac{V+u}{V}f_{0}[\rm Hz]}$ (答)
(3)


音源の前方の波長$\lambda^{\prime}$は
$\lambda^{\prime}=\dfrac{V-v}{f_{0}}$
に縮みます.
また,観測者が$1\rm s$に受け取る波の長さ$L$は
$L=(V-u)\cdot 1$
以上より,観測者が観測する振動数$f$は
$\eqalign{f&=\dfrac{L}{\lambda^{\prime}}\\&=\dfrac{V-u}{\dfrac{V-v}{f_{0}}}\\&=\dfrac{V-u}{V-v}f_{0}[\rm Hz]}$ (答)
(4)


音源の前方の波長$\lambda^{\prime}$は
$\lambda^{\prime}=\dfrac{V+v}{f_{0}}$
に伸びます.
また,観測者が$1\rm s$に受け取る波の長さ$L$は
$L=(V-u)\cdot 1$
以上より,観測者が観測する振動数$f$は
$\eqalign{f&=\dfrac{L}{\lambda^{\prime}}\\&=\dfrac{V-u}{\dfrac{V+v}{f_{0}}}\\&=\dfrac{V-u}{V+v}f_{0}[\rm Hz]}$ (答)
(5)


音源の前方の波長$\lambda^{\prime}$は
$\lambda^{\prime}=\dfrac{V-v}{f_{0}}$
に縮みます.
また,観測者が$1\rm s$に受け取る波の長さ$L$は
$L=(V+u)\cdot 1$
以上より,観測者が観測する振動数$f$は
$\eqalign{f&=\dfrac{L}{\lambda^{\prime}}\\&=\dfrac{V+u}{\dfrac{V-v}{f_{0}}}\\&=\dfrac{V+u}{V-v}f_{0}[\rm Hz]}$ (答)


コメント
[…] ドップラー効果演習1 問題振動数$f_{0}$の音源をもった青の人と,観測者… […]