
前回の内容はこちらです.
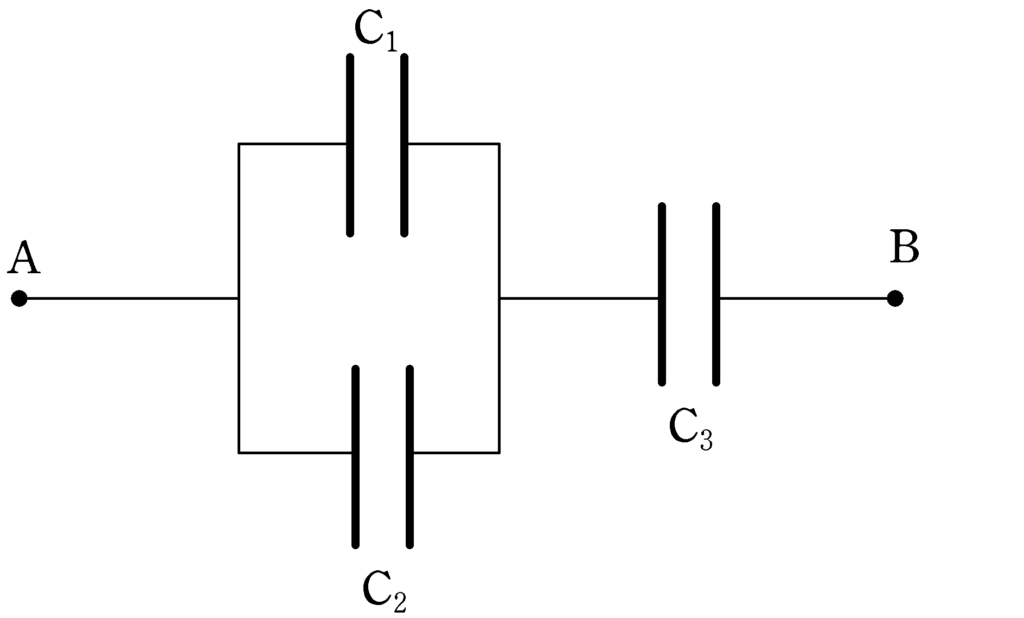
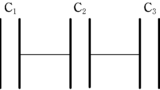
上図のように,帯電していない3つのコンデンサー$\rm C_{1} , C_{2},C_{3}$がある.コンデンサーの電気容量と耐電圧が次の場合であるとき,ABにかけることができる最大電圧はいくらか.
(1) $\rm C_{1}$の電気容量は$C$,耐電圧が$V$,$\rm C_{2}$の電気容量が$C$,耐電圧が$V$,$\rm C_{3}$の電気容量は$C$,耐電圧は$V$.
(2) $\rm C_{1}$の電気容量は$C$,耐電圧が$8V$,$\rm C_{2}$の電気容量が$2C$,耐電圧が$V$, $\rm C_{3}$の電気容量は$3C$,耐電圧は$2V$

直列で電荷が蓄えられてないコンデンサーの場合の電気容量と電圧の比は次のようになります.
次のことは覚えていなくてもいいので,条件を入れて導けるようにしておくとよいです.
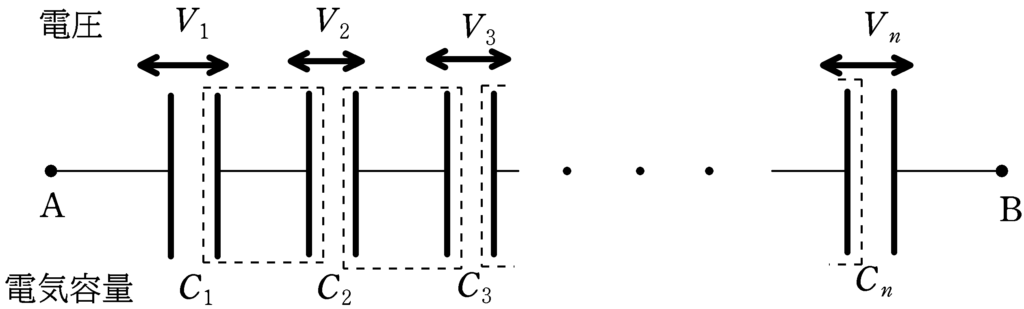
図のような電気容量$C_{1} , C_{2} , C_{3} , \cdots , C_{n}$の$n$個のコンデンサーがある.点線部分の電荷の和が0のとき,AB間に電圧をかけると,どのコンデンサーも蓄えられる電荷が同じなので,電気容量$C$と電圧$V$には
$CV=$一定 すなわち $V=\dfrac{定数}{C}$
の関係がある.つまり,
$V_{1}:V_{2}:\cdots :V_{n}=\dfrac{1}{C_{1}}:\dfrac{1}{C_{2}}:\cdots :\dfrac{1}{C_{n}}$
が成り立つ.

また,今回は並列合成も使います.
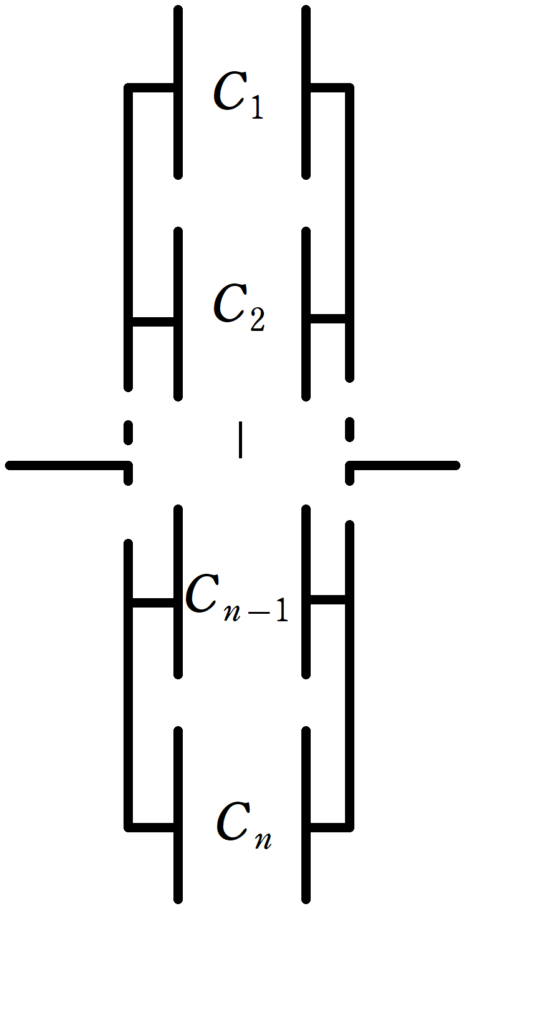
電気容量$C_{1}$,$C_{2}$,$\dots$,$C_{n-1}$,$C_{n}$の$n$個のコンデンサーを並列に結ぶ.
この$n$個のコンデンサーの合成容量$C$は次のような関係式を満たす.
$C=C_{1}+C_{2}+\dots +C_{n-1}+C_{n}$
<解答>
(1)

まずは電圧の比を計算しやすくするために,$\rm C_{1}$と$\rm C_{2}$を並列合成します.合成容量を$C_{12}$とします.
★ 並列合成の式
$C_{12}=C+C=2C$

$\rm C_{1}$と$\rm C_{2}$を合成した方の電圧を$V_{左}$,$\rm C_{3}$の方の電圧を$V_{右}$としましょう.
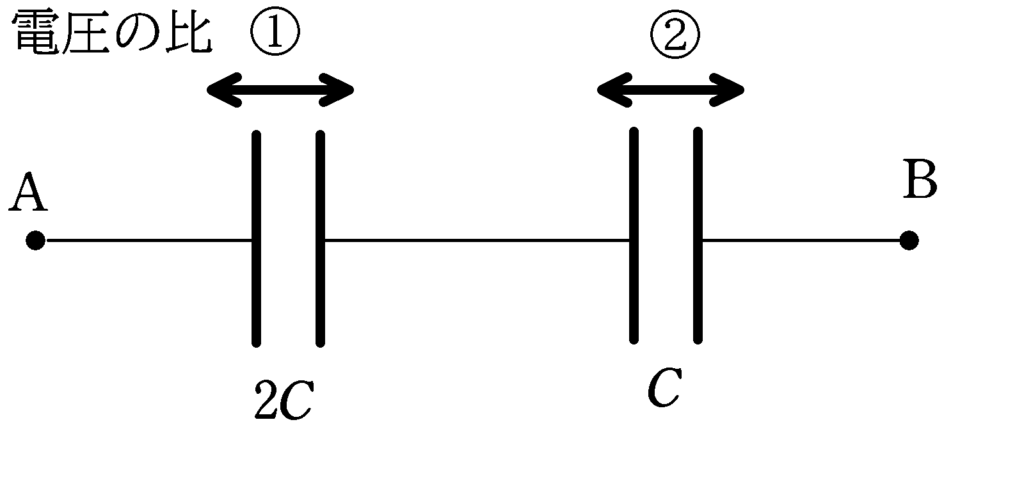
★ 直列コンデンサーの電圧の比
$V_{左}:V_{右}=\dfrac{1}{2C}:\dfrac{1}{C}=1:2$
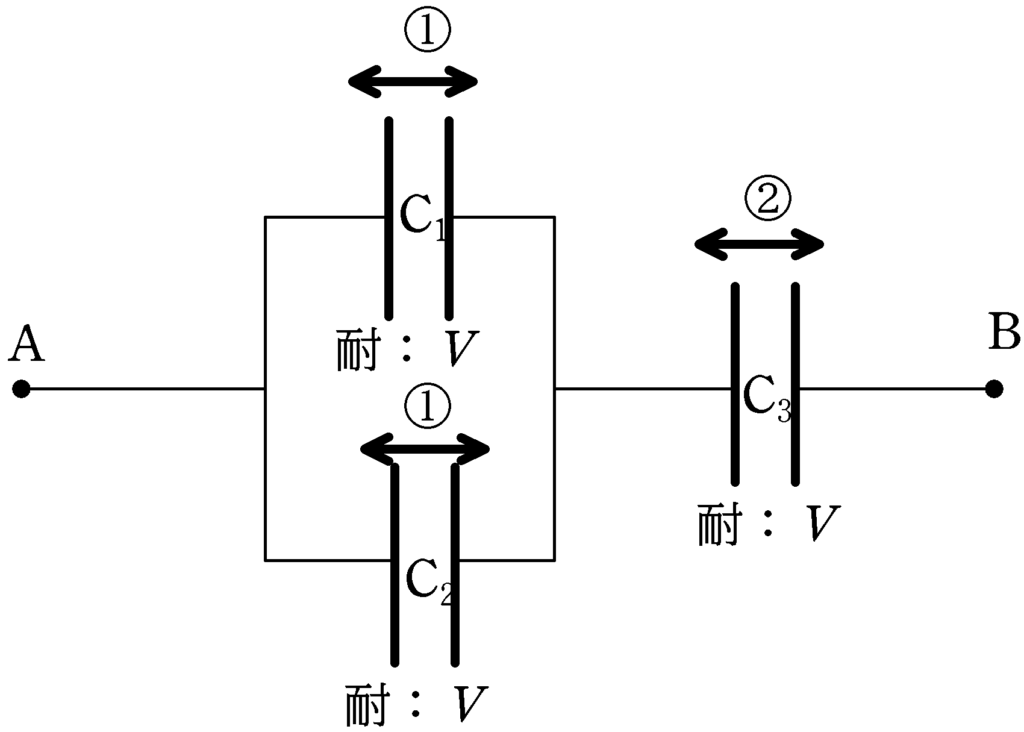

$\rm C_{1}$または$\rm C_{2}$に耐電圧$V$がかかるとすると,$\rm C_{2}$には2倍の$2V$がかかり,これは耐電圧を超えるので不適です.
逆に,$\rm C_{3}$に耐電圧$V$をかけると,$\rm C_{1}$と$\rm C_{2}$には$\dfrac{1}{2}V$の電圧がかかり,これは耐電圧内なので大丈夫です.
よって,AB間の最大電圧は
$\dfrac{1}{2}V+V=\dfrac{3}{2}V$ (答)
(2)

同じく,電圧の比を計算しやすくするために,$\rm C_{1}$と$\rm C_{2}$を並列合成します.合成容量を$C_{12}$とします.
★ 並列合成の式
$C_{12}=2C+C=3C$

$\rm C_{1}$と$\rm C_{2}$を合成した方の電圧を$V_{左}$,$\rm C_{3}$の方の電圧を$V_{右}$としましょう.
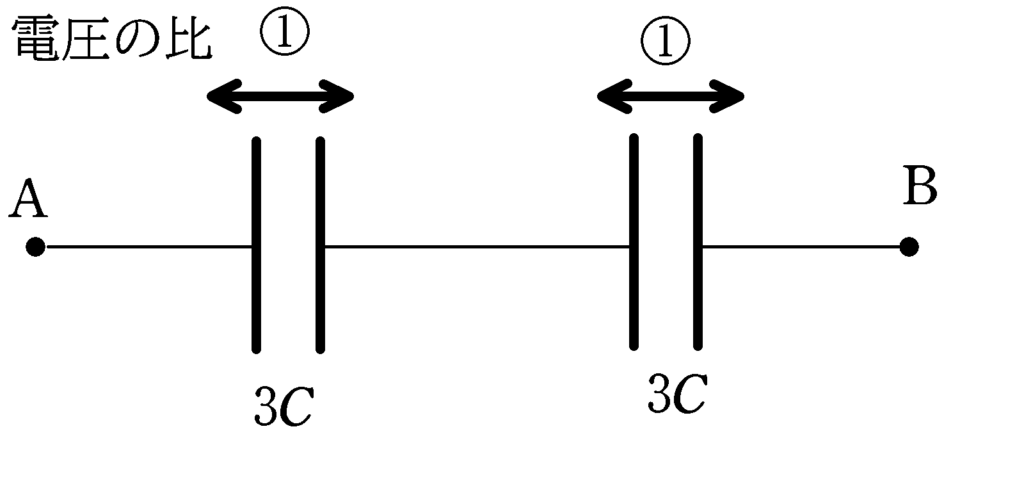
★ 直列コンデンサーの電圧の比
$V_{左}:V_{右}=\dfrac{1}{3C}:\dfrac{1}{3C}=1:1$
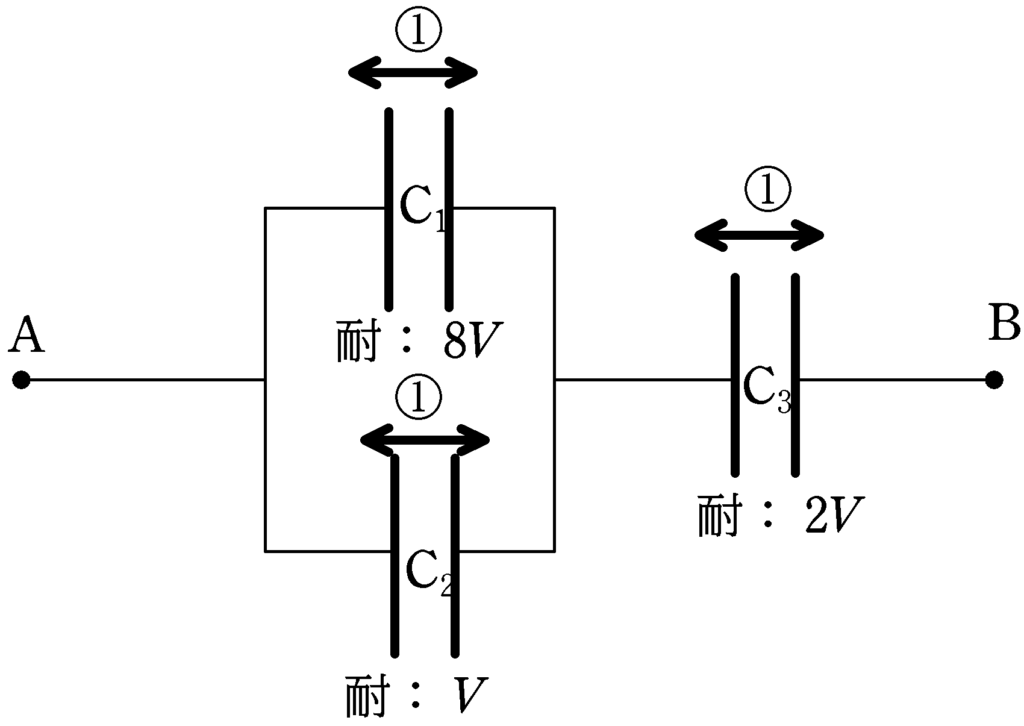

$\rm C_{1} , C_{2}$にかける電圧は最大でも$V$です.(並列の際は同じ電圧がかかるので,耐電圧が小さい方に合わせます.)
このとき,$\rm C_{3}$にかかる電圧は$V$で,これは耐電圧内なので大丈夫です.
このときのAB間の電圧は
$V+V=2V$
また,$\rm C_{3}$の耐電圧$2V$に合わせると,$\rm C_{1} , C_{2}$にも$2V$かかり,これは$\rm C_{3}$の耐電圧を超えるので不適です.
以上より,AB間の最大電圧は
$2V$ (答)


コメント