
今回はコンデンサーが充電する過程を考えていきます.
前半は微分方程式は解かずに説明をし,後半で微分方程式を解いてグラフをかきたいと思います.
入試問題でも意外と出てくるので,対策が必要ですね.
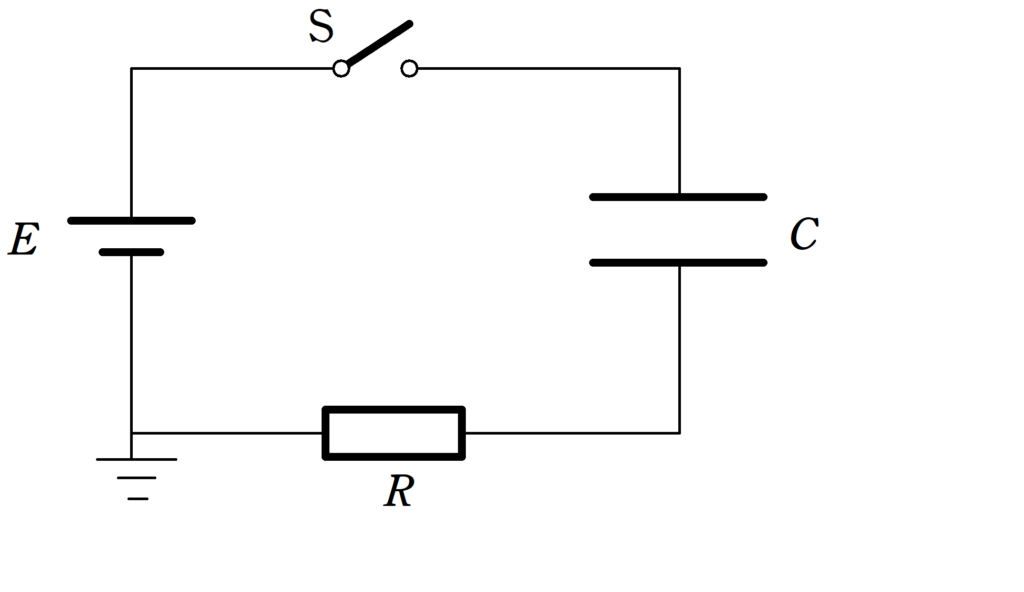

設定は次の通りです.
起電力$E$の電池,スイッチ$\rm S$,電気容量$C$のコンデンサー,抵抗$R$の抵抗器,アースを上図のように設定しましょう.
はじめ,コンデンサーに電荷が蓄えられていない状態からスイッチを閉じて十分時間が経つまでのコンデンサーに蓄えられる電荷の時間変化と電流の時間変化を求めていきましょう.
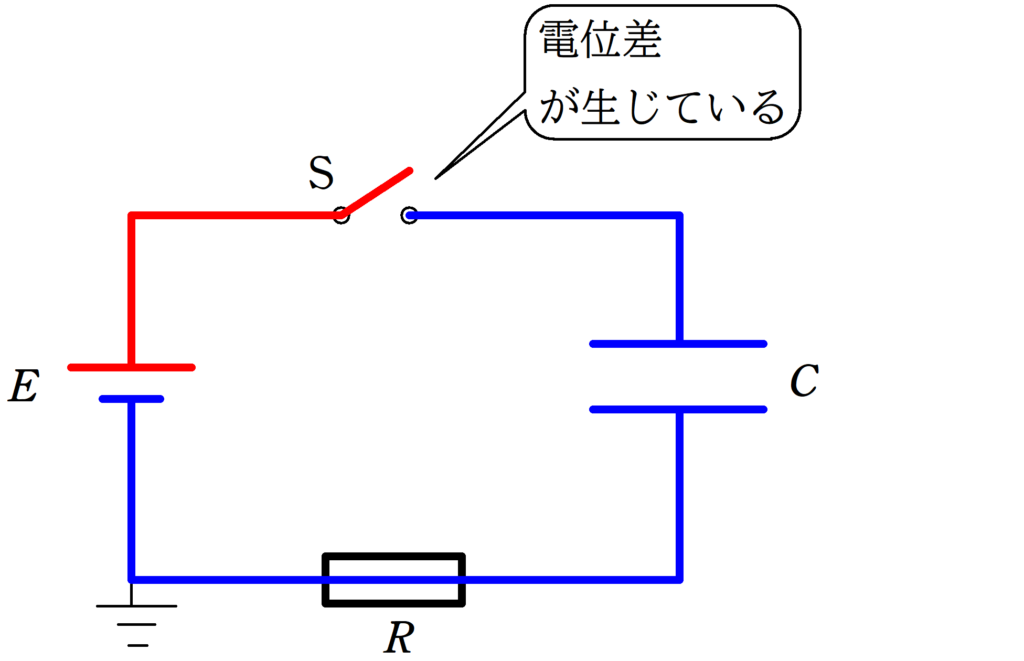

スイッチを閉じる前は,上図のような電位になっています.
青色の電位を$0$とし,赤の電位を$E$としています.
ちなみに,はじめ電荷が蓄えられていない状況なので,コンデンサーの間の電圧は$0$となります.
スイッチを閉じると,電位が高い方から低い方へ電場が生じます.
コンデンサーに蓄えられている電荷を$Q$,コンデンサー間の電圧を$V$とすれば,コンデンサーの電気容量$C$は
$C=\dfrac{Q}{V}$
実際は
$Q=CV$
として使うことが多い.
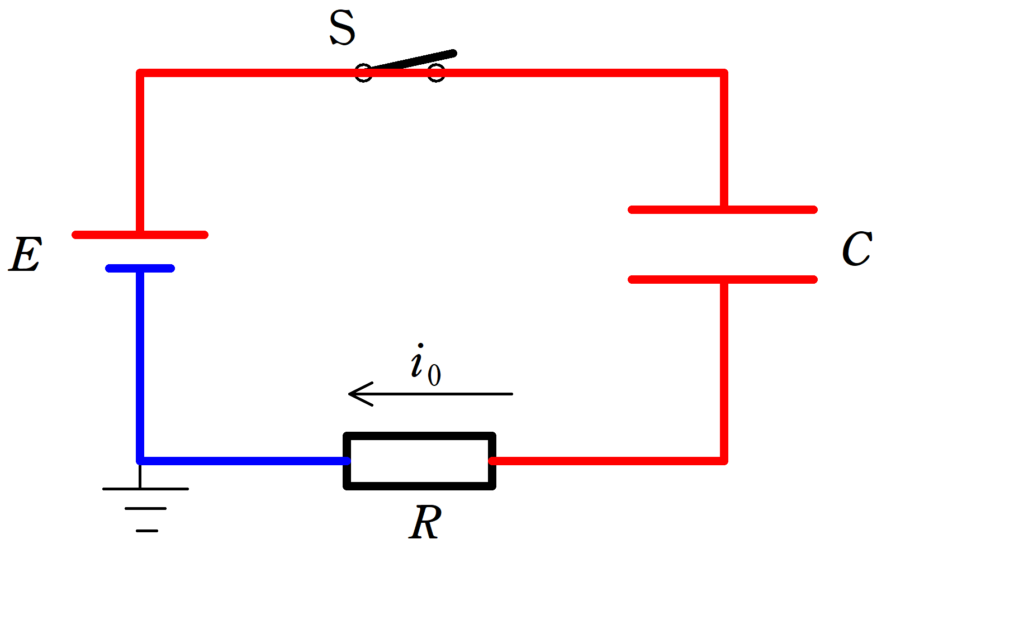

スイッチを閉じた瞬間の電位の状況は次のようになります.
ここで注意して欲しいのが,まだコンデンサーに電荷が蓄えられていないのにも関わらず,回路に電流が流れています.
順序としては,
回路に電流が流れる→コンデンサーに電荷が蓄えられる
なのです.
雨が降る→水がたまる
のようなイメージです.
抵抗器に着目すると,抵抗器の電圧が$E$となっていて,抵抗が$R$なので,流れる電流$i_{0}$は,オームの法則より
$i_{0}=\dfrac{E}{R}$
となります.
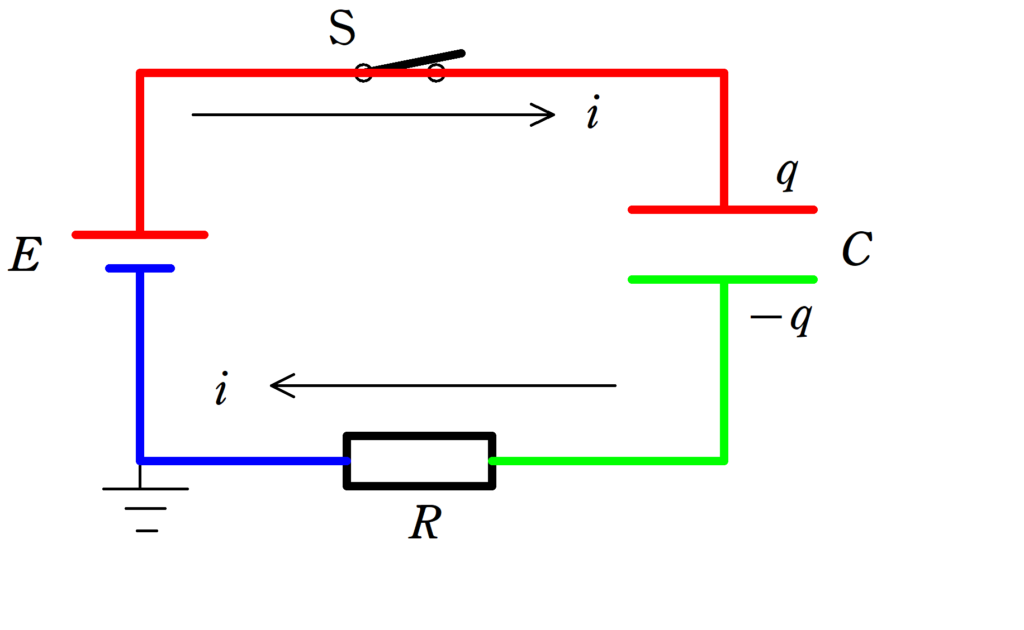

途中経過を考えましょう.
電流が流れるとコンデンサーに電荷が運ばれます.
コンデンサーに蓄えている電荷を$q$として,この瞬間に回路に流れている電流を$i$とします.
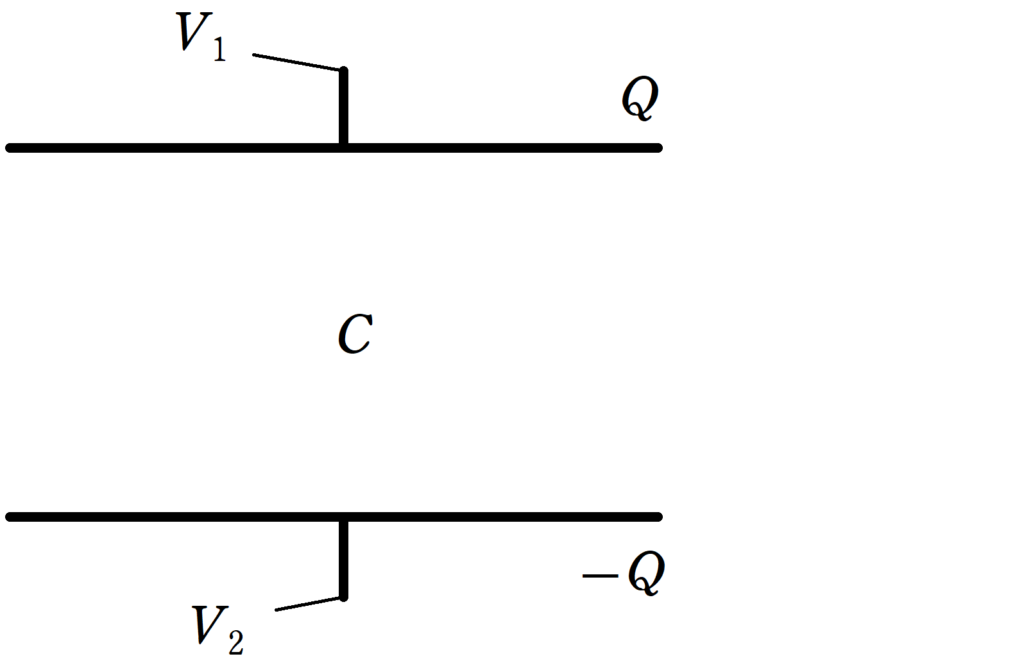
電気容量$C$のコンデンサーに,電荷$Q$が蓄えれている.
$+Q$側の極板の電位を$V_{1}$,$-Q$側の極板の電位を$V_{2}$とすると,コンデンサーの式より
$Q=C(V_{1}-V_{2})$
であるから,
$V_{1}-V_{2}=\dfrac{Q}{C}$
の電位差が生じている.

すると,キルヒホッフ則は次のようになります.
$E-\dfrac{q}{c}-Ri=0$ $\dots (\ast)$
$i$は次の電流の定義式で変形できます.
時間$\Delta t$の間に電気量$\Delta Q$が通過するときの電流の大きさ$i$は
$i=\dfrac{\Delta Q}{\Delta t}$

$i=\dfrac{\Delta q}{\Delta t}$
したがって,$(\ast)$は
$E-\dfrac{q}{C}-R\dfrac{\Delta q}{\Delta t}=0$
これを次のように変形しましょう.
$\dfrac{\Delta q}{\Delta t}=-\dfrac{1}{RC}q+\dfrac{E}{R}$

$\dfrac{\Delta q}{\Delta t}=-\dfrac{1}{RC}q+\dfrac{E}{R}$ $\dots (2\ast)$
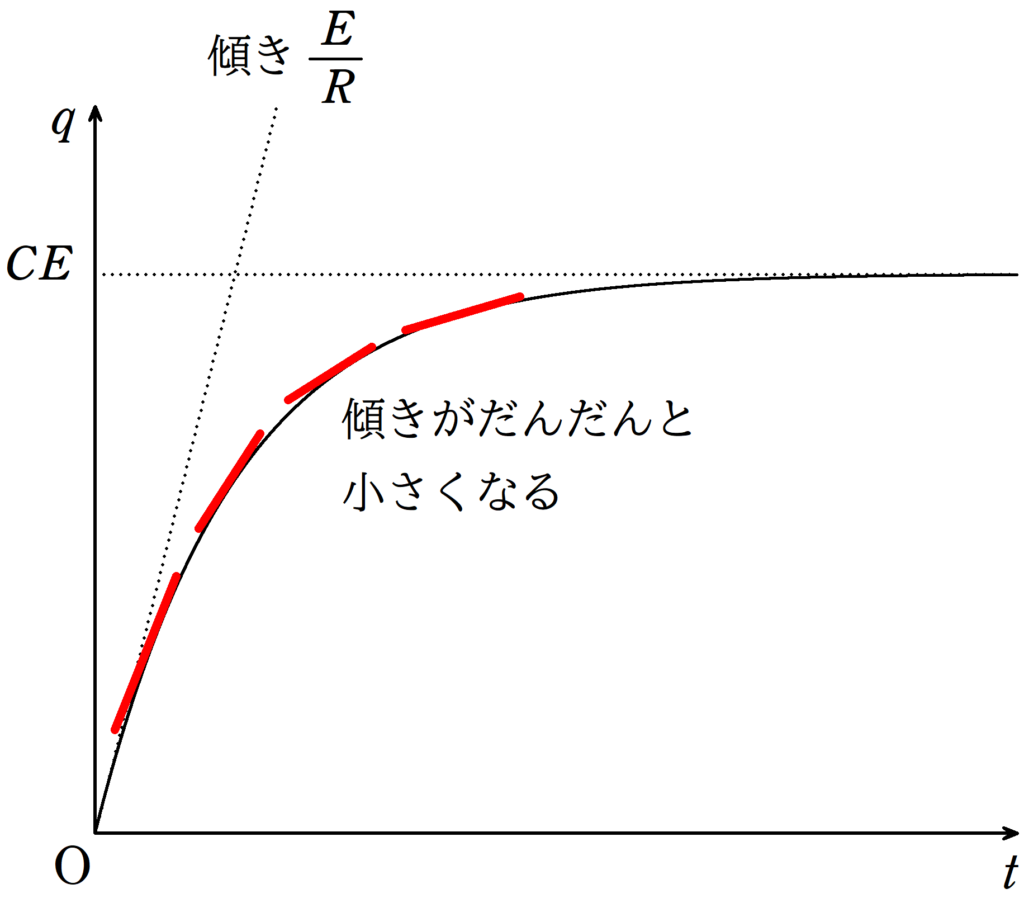
から,縦軸が$q$,横軸が$t$のグラフを描いてみます.
$\dfrac{\Delta q}{\Delta t}$は$q-t$グラフの傾きを表します.
$t=0$のとき,$q=0$より,$(2\ast)$に代入して
$\dfrac{\Delta q}{\Delta t}=\dfrac{E}{R}$
つまり,$t=0$の$q-t$グラフの傾きは$\dfrac{E}{R}$となります.
しかし,このままで傾きが一定になるわけではありません.
$\dfrac{\Delta q}{\Delta t}=-\dfrac{1}{RC}q+\dfrac{E}{R}$
によると,$q$が増えれば増えるほど,右辺が小さくなり,したがって,$\dfrac{\Delta q}{\Delta t}$が小さくなります.
そして,十分時間が経つと,ついには$\dfrac{\Delta q}{\Delta t}$は$0$になってしまいます.
$(2\ast)$に$\dfrac{\Delta q}{\Delta t}=0$を代入すると,
$0=-\dfrac{1}{RC}q+\dfrac{E}{R}$
$\therefore q=CE$
つまり,最終的にはコンデンサーには電荷$CE$の電荷が蓄えられます.

今度は回路の式から微分方程式を解いてみましょう.
今回の微分方程式は,こちらの記事でも紹介しています.

★ 回路の式
$E-\dfrac{q}{C}-Ri=0$
$i=\dfrac{dq}{dt}$を代入して
$E-\dfrac{q}{C}-R\dfrac{dq}{dt}=0$
これを次のように変形する.
$\dfrac{dq}{dt}=-\dfrac{1}{RC}(q-CE)$ $\dots (3\ast)$
$y$が$t$の関数であるとする.$\lambda$を定数としたとき,$y$は次の微分方程式を満たす.
$\dfrac{dy}{dt}=\lambda y$
このとき,積分定数を$K$とすると,上の微分方程式の解は次のようになる.
$y=Ke^{\lambda t}$
ただし,$e$は自然対数の底である.
$q^{\prime}=q-CE$とおくと,$\dfrac{dq^{\prime}}{dt}=\dfrac{dq}{dt}$より$(3\ast)$を変形して
$\dfrac{dq^{\prime}}{dt}=-\dfrac{1}{RC}q^{\prime}$
積分定数を$K$として,この微分方程式を解くと
$q^{\prime}=Ke^{-\frac{1}{RC}t}$
$q^{\prime}=q-CE$を戻して
$q-CE=Ke^{-\frac{1}{RC}t}$
$\therefore q=CE+Ke^{\frac{1}{RC}t}$ $\dots (\spadesuit)$

積分定数$K$を初期条件を入れて,決定しましょう.
今回の問題では,$t=0$のとき,コンデンサーに電荷は蓄えられていないので,$q=0$.
これを$(\spadesuit)$に代入して
$0=CE+Ke^{0}$
$\therefore K=-CE$
$K=-CE$を$(\spadesuit)$に代入すると
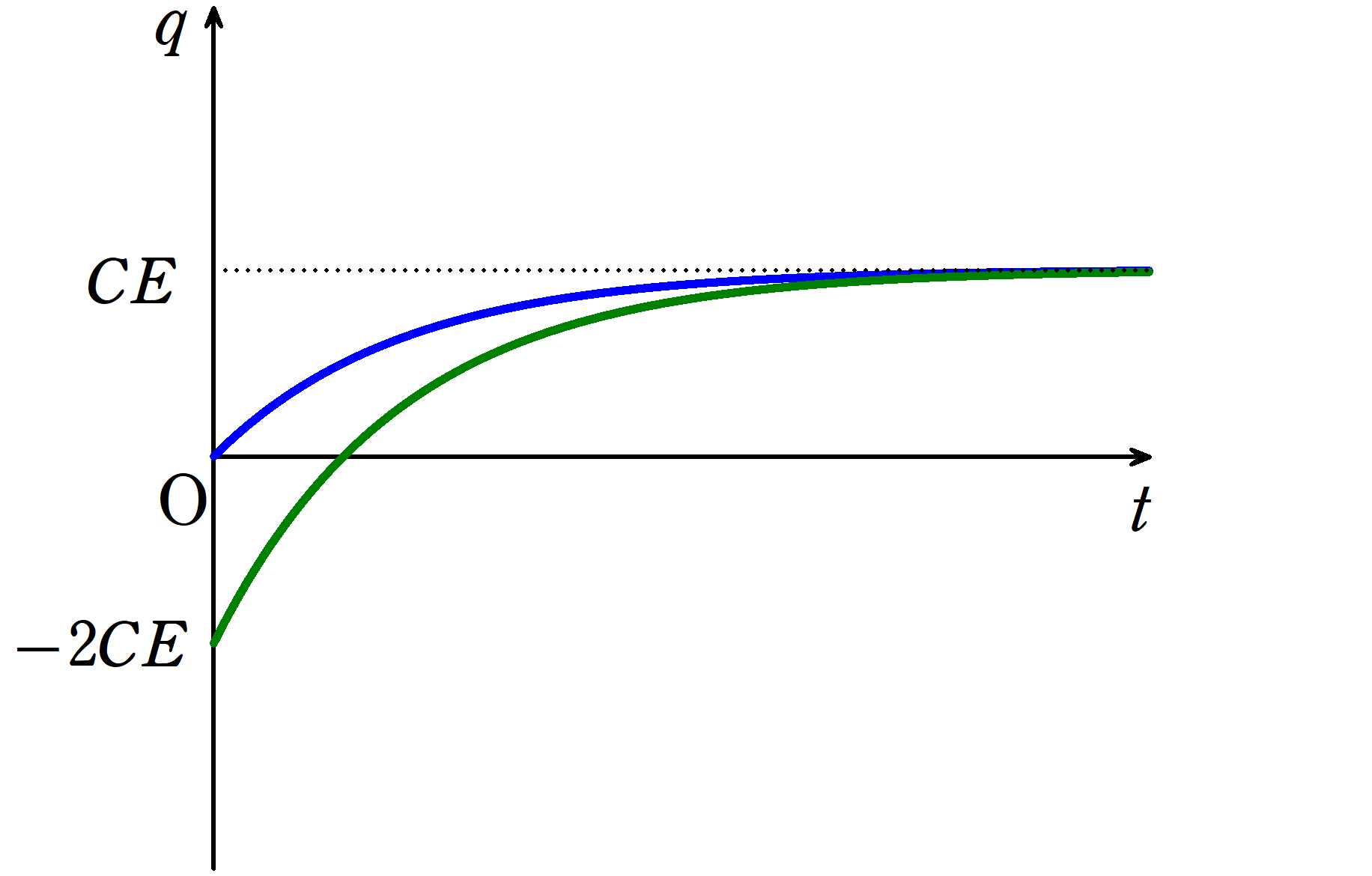
$q=CE-CEe^{-\frac{1}{RC}t}$ $\dots (4\ast)$
$i=\dfrac{dq}{dt}$より,
$\eqalign{i&=-CE\cdot (-\dfrac{1}{RC})e^{-\frac{1}{RC}t}\\&=\dfrac{E}{R}e^{-\frac{1}{RC}t}}$ $\dots (5\ast)$
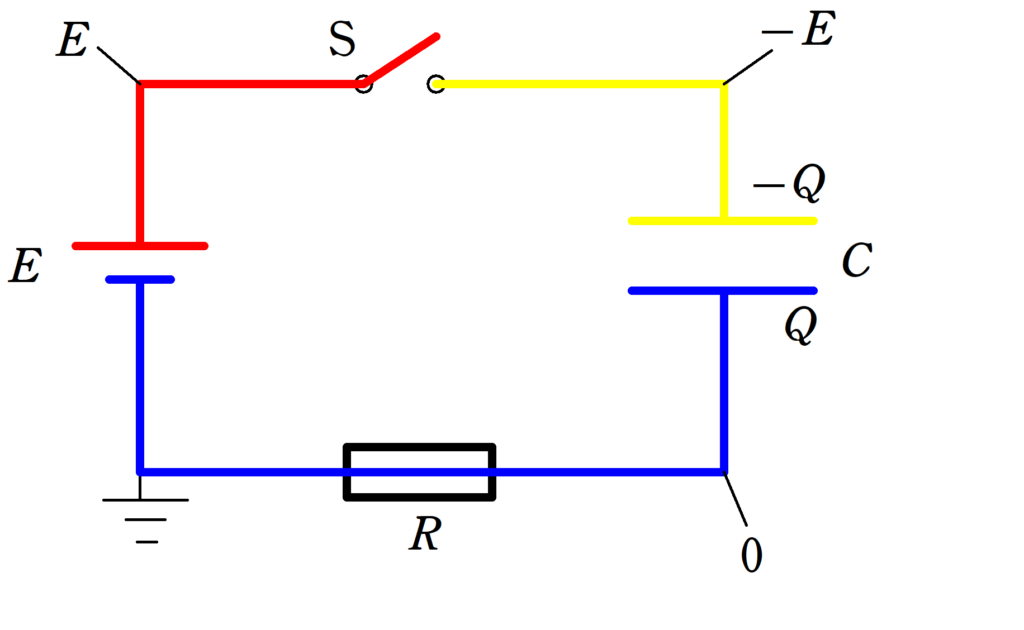

また,初期条件を変えるとどうなるのでしょうか?
たとえば,$Q=CE$の電荷を上図のように帯電した状態からスイッチを閉じます.
すると,$(\spadesuit)$において,$t=0$のとき,$q=-CE$を代入して
$-CE=CE+Ke^{0}$
$\therefore K=-2CE$
これを再び$(\spadesuit)$に代入すると,
$q=CE-2CEe^{-\frac{1}{RC}t}$ $\dots (6\ast)$
$i=\dfrac{dq}{dt}$より,
$\eqalign{i&=-2CE\cdot (-\dfrac{1}{RC})e^{-\frac{1}{RC}t}\\&=\dfrac{2E}{R}e^{-\frac{1}{RC}t}}$ $\dots (7\ast)$
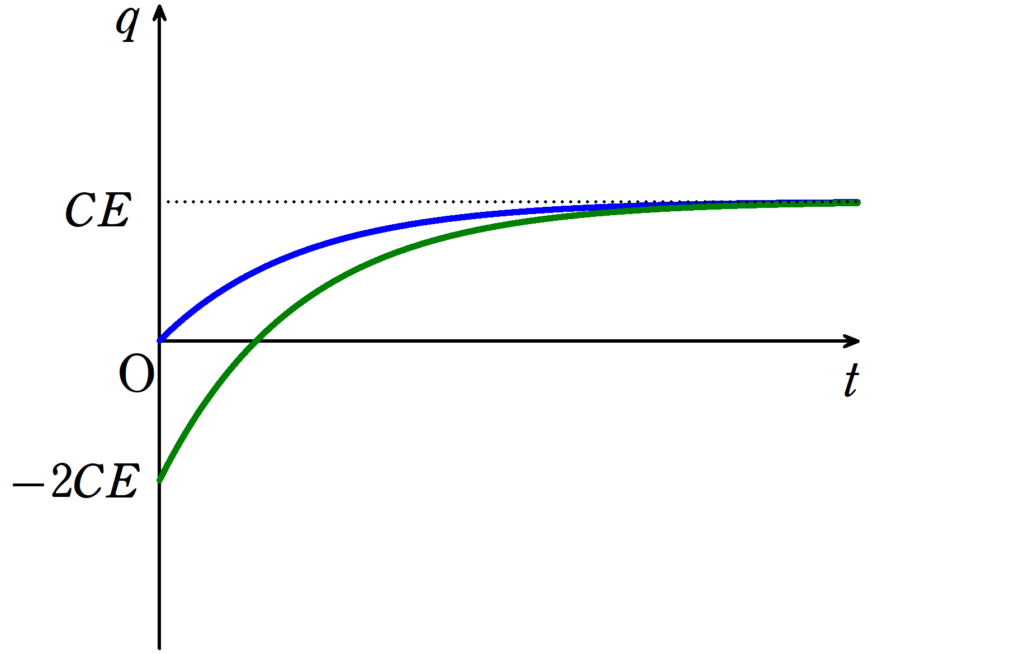

上図において,$(4\ast)$が青のグラフで,$(6\ast)$が緑のグラフです.
結局はどちらも$Q=CE$に落ち着きますね.
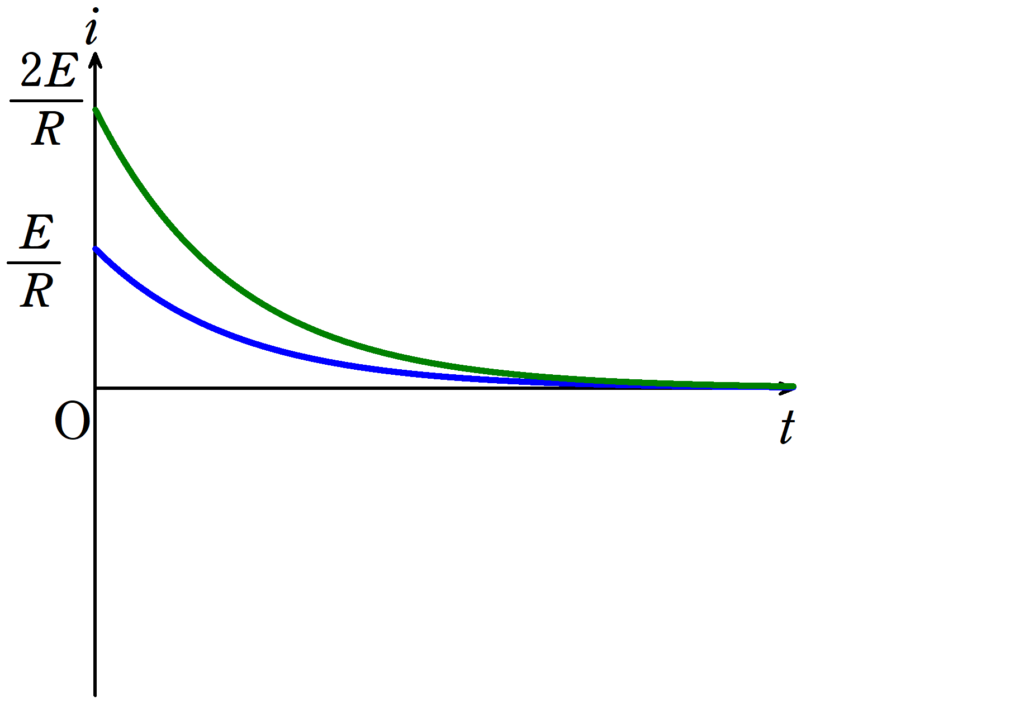

上図において,$(5\ast)$が青のグラフ,$(7\ast)$が緑のグラフです.
どちらも最終的には電流が流れていませんね.



コメント
[…] [過渡現象]コンデンサーの充電 […]