<問題>
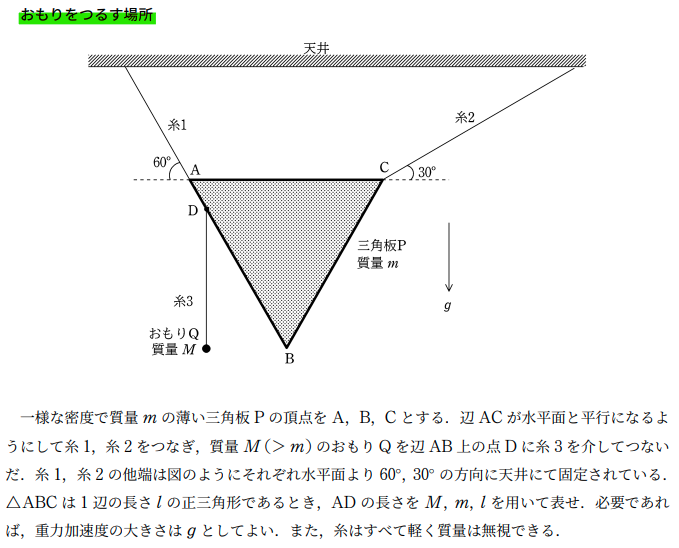
<解答>
張力の大きさを設定して,
①鉛直方向のつり合い ②水平方向のつり合い ③力のモーメントのつり合い(たとえばAを中心にする)
を立てることでADの長さを計算することができますが,ここでは力のモーメントのつり合いの式は立てずに計算してみたいと思います.(入試では途中経過が聞かれたりすることも多いので,上のやり方ができる人はそれでOKです.こんなやり方もありますという紹介です.)
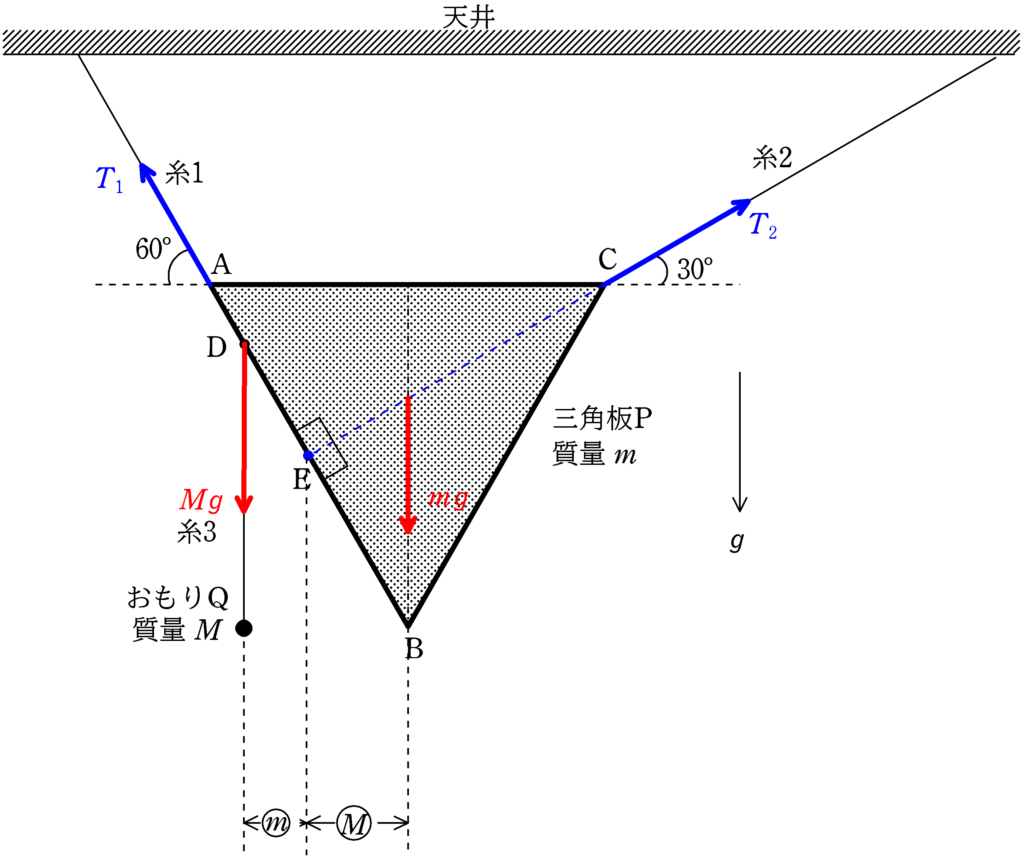
上図のように,糸1と糸2が三角台Pにおよぼす張力の作用線は上図の点Eで交わります.
そこで次のことを使います.
剛体がつり合っているとき,3力以上の平行でない作用線は一点で交わる.これを用いて,次のよううなことを求めることができる.
- 力の作用線の向き
- 力の作用点の位置(特に転倒問題でよく使う)
作用線が一点で交わるためには点Dにはたらく大きさ$Mg$の張力と三角台Pの重力$mg$の合力が上図の点Eを通る鉛直線になくてはいけません.

上図のように,A点とB点にそれぞれ平行で同じ向きに,大きさ$F_{1}$と$F_{2}$の力がかかっているとします.このとき,A点にはたらく力とB点にはたらく力を合成すると
- 向き→2つの力と同じ向き
- 大きさ$F_{1}+F_{2}$
- 合力の始点→ABを$F_{2}:F_{1}$に内分した点P(つまり,2力の逆比)
これは,重心の考え方を利用すればすぐに計算できるのでわざわざ覚える必要もありませんが,結局重心の計算をするときに自ずと覚えてしまっているかもしれません.
$Mg$の力と$mg$の力の合力は線分DEを$m:M$に内分した点です.
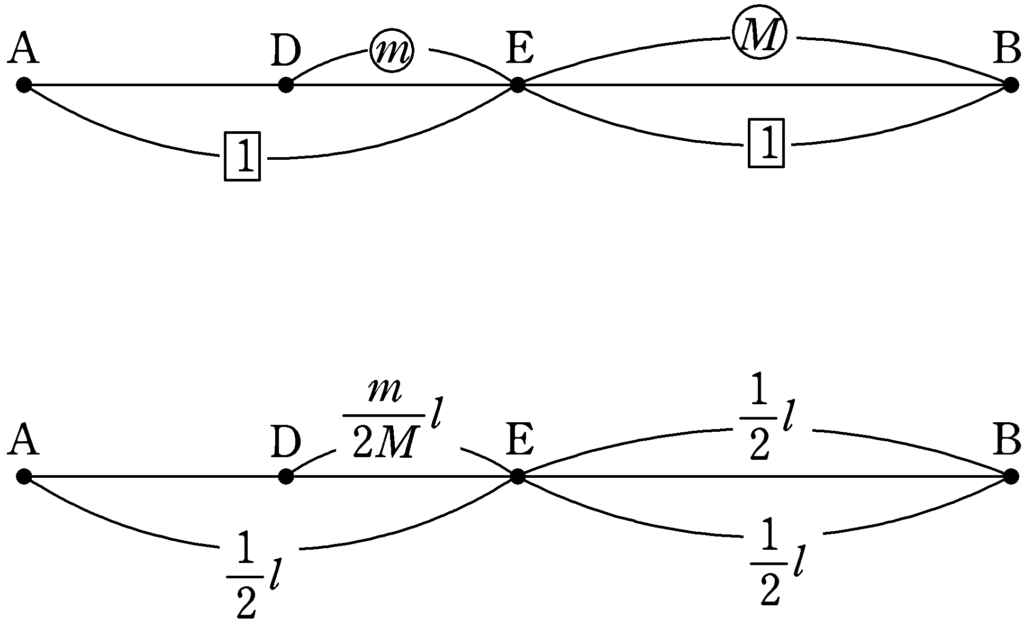
今回はたまたまEが線分ABの中点にあるので,上図のようにEB$=\dfrac{1}{2}l$とわかり,DEの長さは
${\rm DE}:\dfrac{1}{2}l=m:M$ $\therefore\,\,{\rm DE}=\dfrac{m}{2M}l$
となります.ABの長さが$l$なので,AD$=x$とすると
$x=l-\dfrac{m}{2M}l-\dfrac{1}{2}l=\dfrac{M-m}{2M}l$ (答)
となります.



コメント