
今回は2題あります.
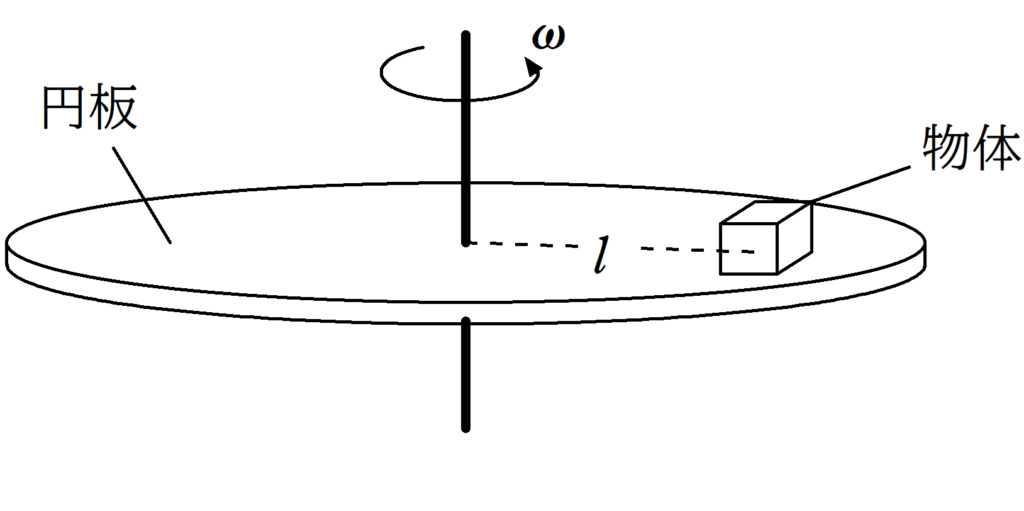
図のように,粗い上面をもつ円板の上に物体がおかれている.円板の中心から物体の重心までの距離は$l$であった.この状態から円板をゆっくりと回転させて,その角速度を少しずつ大きくした.角速度$\omega$になったときに物体が円板上を滑り出した.このとき,次の問いに答えよ.ただし,重力加速度の大きさを$g$として,静止摩擦係数を$\mu$とする.また,円板の上面は水平面と平行である.
(1) 円運動の運動方程式を立てよ.
(2) $\omega$を$\mu$,$g$,$l$を用いて表せ.
<解答>
(1)

物体が等速円運動をしている事実から物体には向心力がはたらくことがわかります.
円板の面に平行な力は摩擦力しかありません.
そこで,摩擦力が中心方向にはたらくと考えます.
実は問題によっては摩擦力の向きは必ずしも中心を向くとは限りません.
力をとりあえず設定して,運動方程式やつり合いの式を立てて,計算します.
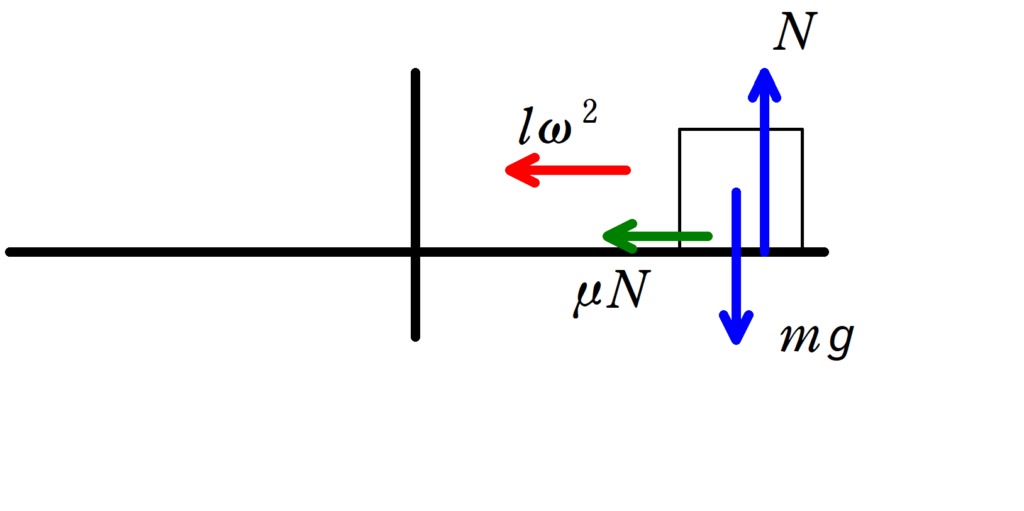

問題文の条件から,物体には最大静止摩擦力がはたらきます.
物体にはたらく鉛直方向の力は重力と垂直抗力のみでつり合っているので,垂直抗力の大きさ$N$は$N=mg$となります.
したがって,最大静止摩擦力の大きさは$\mu N=\mu mg$です.
向心方向の運動方程式を立てましょう.
半径$r$,円運動の接線方向の速さを$v$,角速度を$\omega$とすると,向心加速度の大きさ$a$は
$a=\dfrac{v^{2}}{r}=r\omega^{2}$
向心加速度の向きは円運動の中心
★ 向心方向の運動方程式
$ml\omega^{2}=\mu mg$ (答) $\dots (\ast)$
(2) $(\ast)$により
$\omega=\sqrt{\dfrac{\mu g}{l}}$ (答)
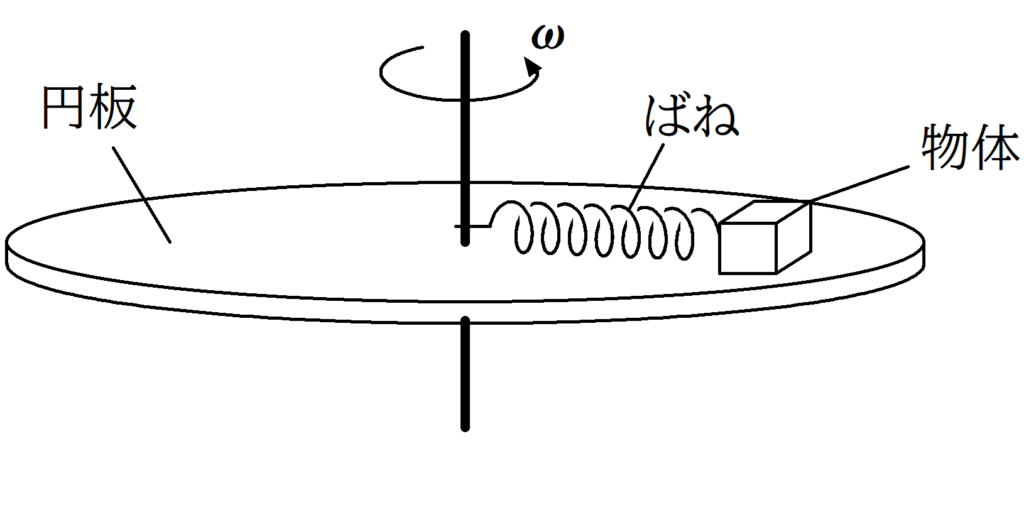
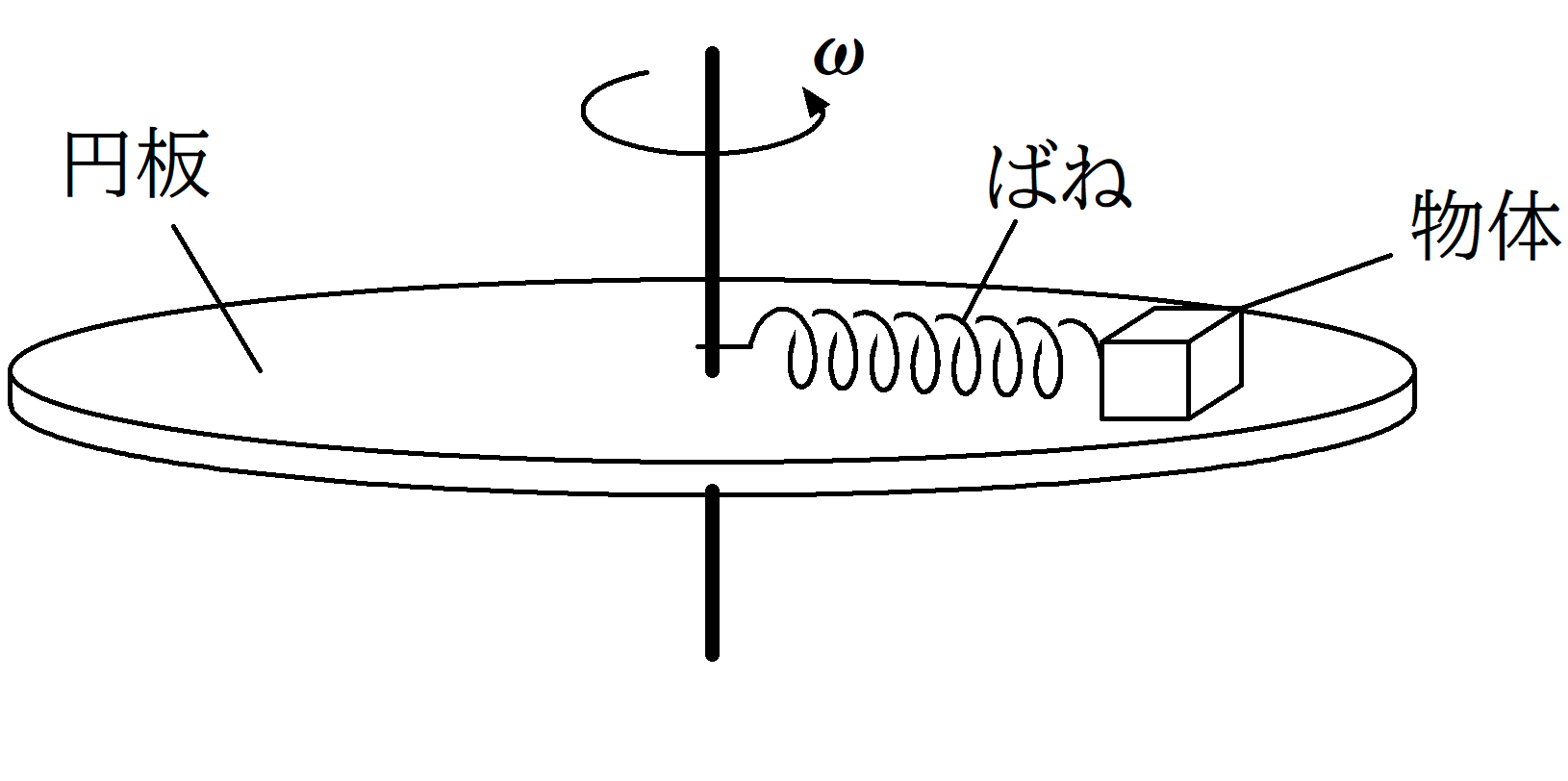
図のように,なめらかな上面をもつ円板に質量$m$の物体がおかれている.物体には,自然長$l_{0}$でばね定数$k$のばねがつながれている.円板を角速度$\omega$で回転させておいた上で,物体に力を加え,ばねを伸ばしては物体から静かに手をはなす実験をした.ばねの長さ$l$が$l_{0}\leqq l<l_{1}$の範囲では物体は円板に対して動き出してしまったが,$l=l_{1}$のときは物体は円板に対してちょうど静止した.ただし,$k>m\omega^{2}$とする.このとき,次の問いに答えよ.
(1) $l=l_{1}$のとき,物体の円運動の運動方程式を立てよ.
(2) $l_{1}$を$k$,$\omega$,$m$,$l_{0}$を用いて表せ.
<解答>
(1)
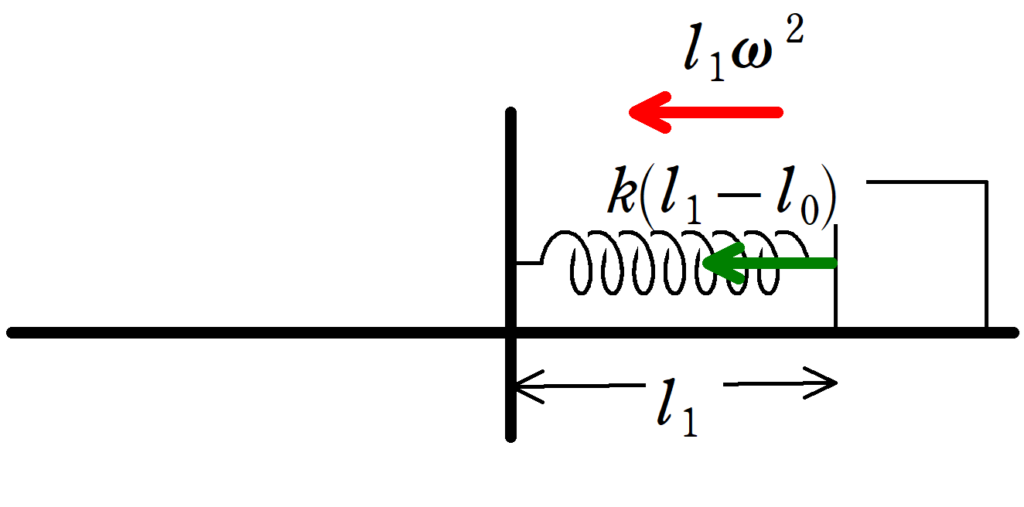

弾性力が向心力となって円運動をします.
半径が$l_{1}$の円運動なので,向心加速度は中心向きに$l_{1}\omega^{2}$ですが,弾性力の大きさは(ばね定数)×(自然からの伸び or 縮み)なので,その大きさは,$k(l_{1}-l_{0})$です.
ときどき,弾性力を$kl_{1}$としてしまう人をみかけるので注意してください.
それでは,向心方向の運動方程式を立てましょう.
★ 向心方向の運動方程式
$ml_{1}\omega^{2}=k(l_{1}-l_{0})$ (答) $\dots (2\ast)$
(2) $(2\ast)$より
$(k-m\omega^{2})l_{1}=kl_{0}$
$\therefore l_{1}=\dfrac{k}{k-mw^{2}}l_{0}$ (答)

コメント