[基本]円運動演習2　円錐容器内の運動

問題

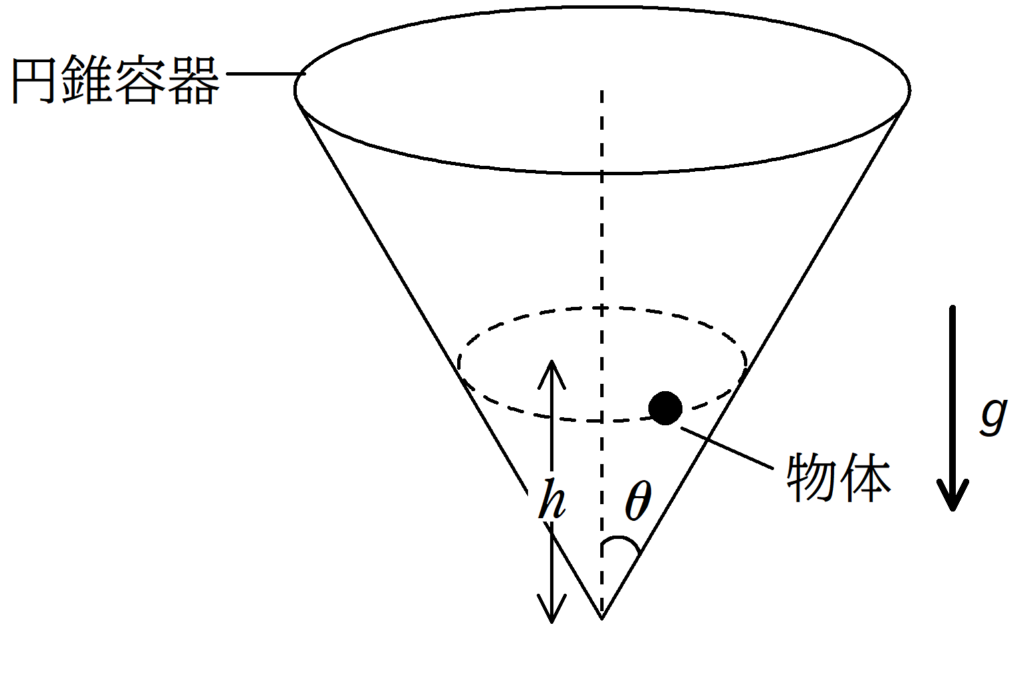
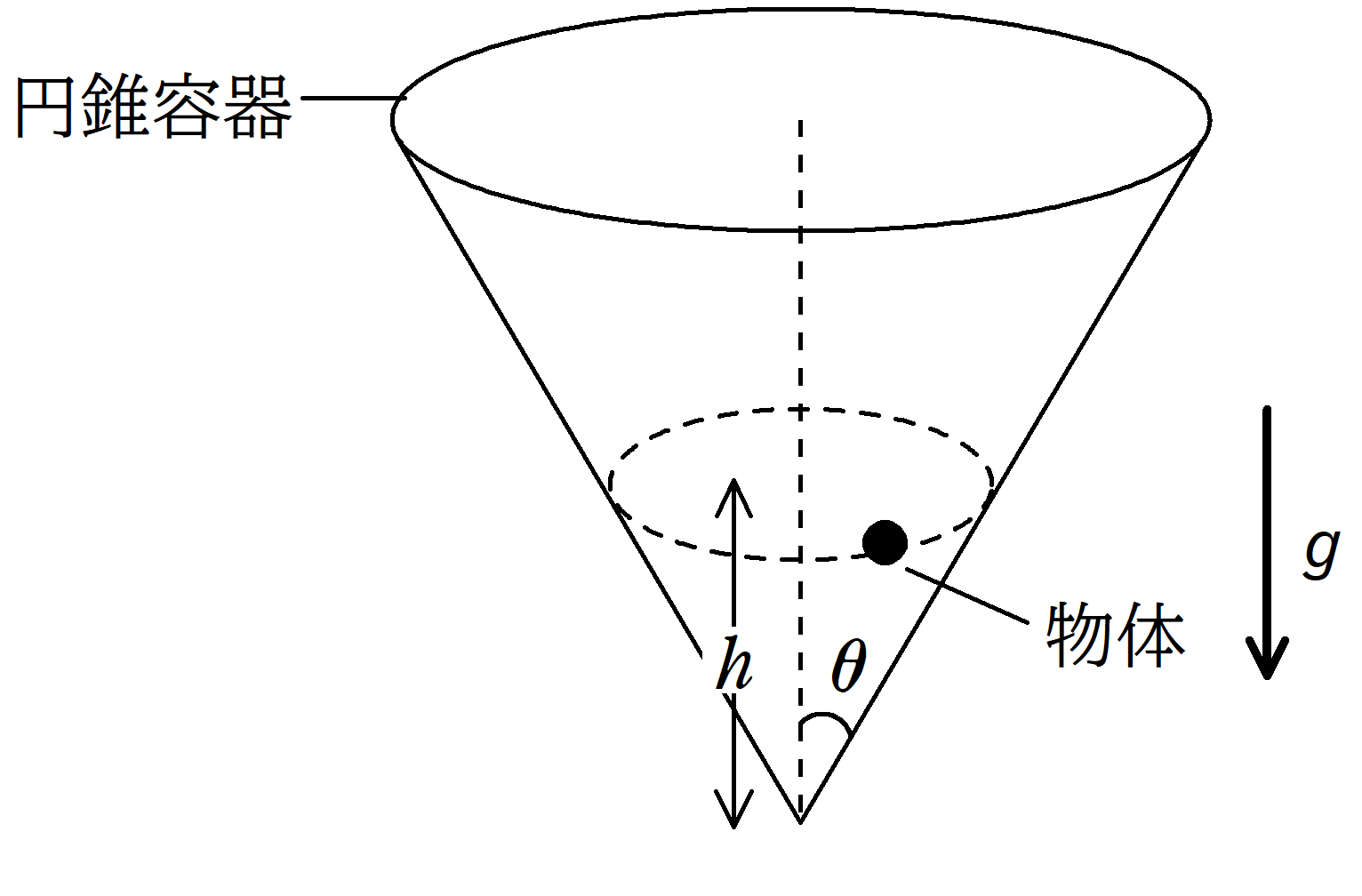
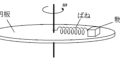
上図のように半頂角が$\theta$の円錐容器を円錐の頂点を水平面に固定し，円錐容器の底面が水平面と平行になるようにした．次に，質量$m$の物体を円錐容器の内部で角速度$\omega$の等速円運動をさせた．円軌道の面は水平面と平行にあり，水平面から円軌道面までの距離は$h$である．円錐容器の厚さは無視をし，円錐容器内部はなめらかである．重力加速度の大きさを$g$として，次の問いに答えよ．

(1)　物体が円錐容器より受ける垂直抗力の大きさを$N$とする．物体の円運動の運動方程式と鉛直方向のつり合いの式をそれぞれ立てよ．

(2)　円運動の周期$T$を$h$，$\theta$，$g$の中から必要なものを用いて表せ．

＜解答＞

(1)

NEKO

等速円運動の問題で立てて欲しいのは次の2式です．

NEKO

それでは，向心方向の運動方程式と鉛直方向のつり合いの式をそれぞれ立てていきます．

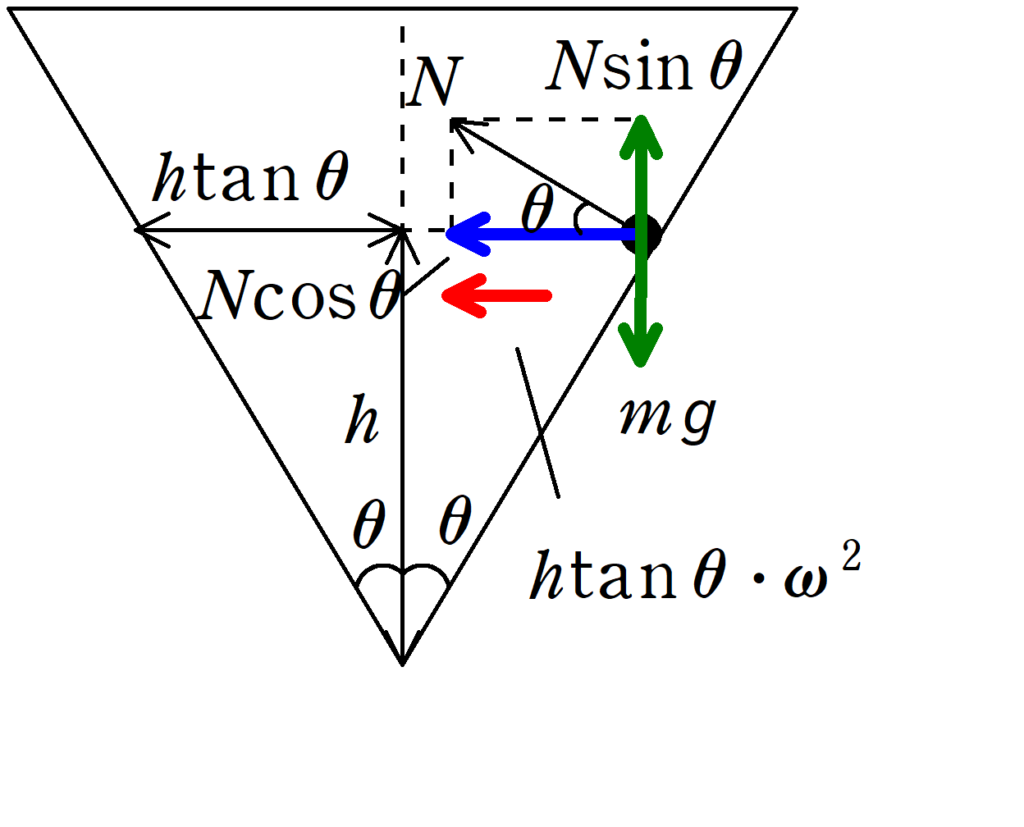
鉛直方向にはたらく力（下図緑色）は，鉛直上向きに$N\sin\theta$，鉛直下向きに$mg$，向心方向の力（下図青色）は，$N\cos\theta$です．

そして，向心加速度は$h\tan\theta\cdot \omega^{2}$です．（円運動の半径は$h\tan\theta$です．）

★　鉛直方向のつり合いの式

$N\sin\theta=mg$　(答)　

$\therefore　N=\dfrac{mg}{\sin\theta}$　$\dots　(\ast)$

★　向心方向の運動方程式

$mh\tan\theta\cdot \omega^{2}=N\cos\theta$　(答)　$\dots　(2\ast)$

(2)

NEKO

$(\ast)$，$(2\ast)$の式より，$N$を消去します．（(2)で答える文字に含まれていないため）

$(\ast)$，$(2\ast)$より

$mh\tan\theta\cdot \omega^{2}=\dfrac{mg}{\sin\theta}\cdot \cos\theta$

$\therefore　\omega=\sqrt{\dfrac{g}{h\tan^{2}\theta}}$　$\dots　(3\ast)$

周期の式より

$\eqalign{T&=\dfrac{2\pi}{\omega}\\&=2\pi\tan\theta\sqrt{\dfrac{h}{g}}}$　(答)