
今回から発展問題を扱います.
本日は,1つのばねに2つの物体が取り付けられた際の単振動の問題です.
かなり複雑な運動をしますが,観測者を変えることで,簡単な運動の組み合わせと考えることができます.

では,さっそく問題を見てみましょう!
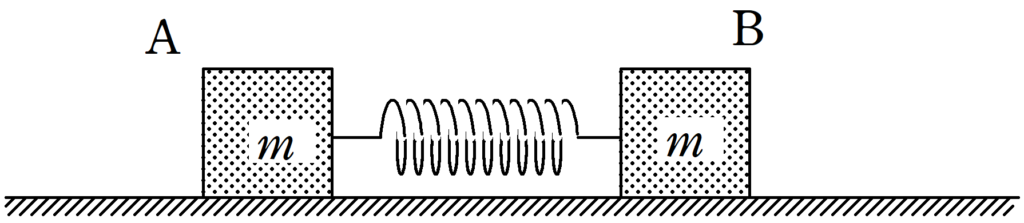
図のように水平で滑らかな床の上に質量$m$の2つ物体A,Bがばね定数$k$の軽いばねによってつながれている.
自然長の状態からAとBに力を加えてばねを$2l$だけ伸ばして静かにはなした.
その後の運動について,次の問いに答えよ.
(1) 任意の時刻におけるAとBの重心の速度を求めよ.
(2) 重心からみたBの運動を考える.このとき,ばねの長さはもとの半分になっている.このことから,重心と物体Bの間のばね定数を求めよ.
(2)のとき,最初Bは重心からみて自然長から$l$だけ伸びている.自然長の位置を原点として,ばねが伸びる方向に$x$座標をとる.両物体を静かにはなした時刻を$t=0$として,時刻$t$における重心から見た物体Bの座標を求めたい.
(3) 物体Bが座標$x$にいるときの加速度を$a$とする.このときの物体Bの運動方程式を立てよ.
(4) (3)より,時刻$t$における位置$x$の式を求めよ.
<解答>
(1)

重心の運動を知るには,重心の運動方程式を立てればいいんだったね.
質量$m_{1}$,$m_{2}$の物体の重心の加速度を$a_{\rm G}$とする.2つの物体にはたらいている力をそれぞれ$F_{1}$,$F_{2}$とすると,次の式が成り立つ.
$(m_{1}+m_{2})a_{\rm G}=F_{1}+F_{2}$

この問題では,物体A,Bにはたらく力は弾性力のみだね.
つまり,力の和はつねに0だね.
だから,重心の運動方程式は次のようになるよ.
★ 重心の運動方程式
$(m+m)a_{\rm G}=0$ $\therefore a_{\rm G}=0$

重心の加速度は0だね.
重心が速度の変化は0ということは,もともと,AとBの物体は静止していて,重心も静止していたので,重心速度はずっと0となるよ.
答え 重心速度は0
(2)

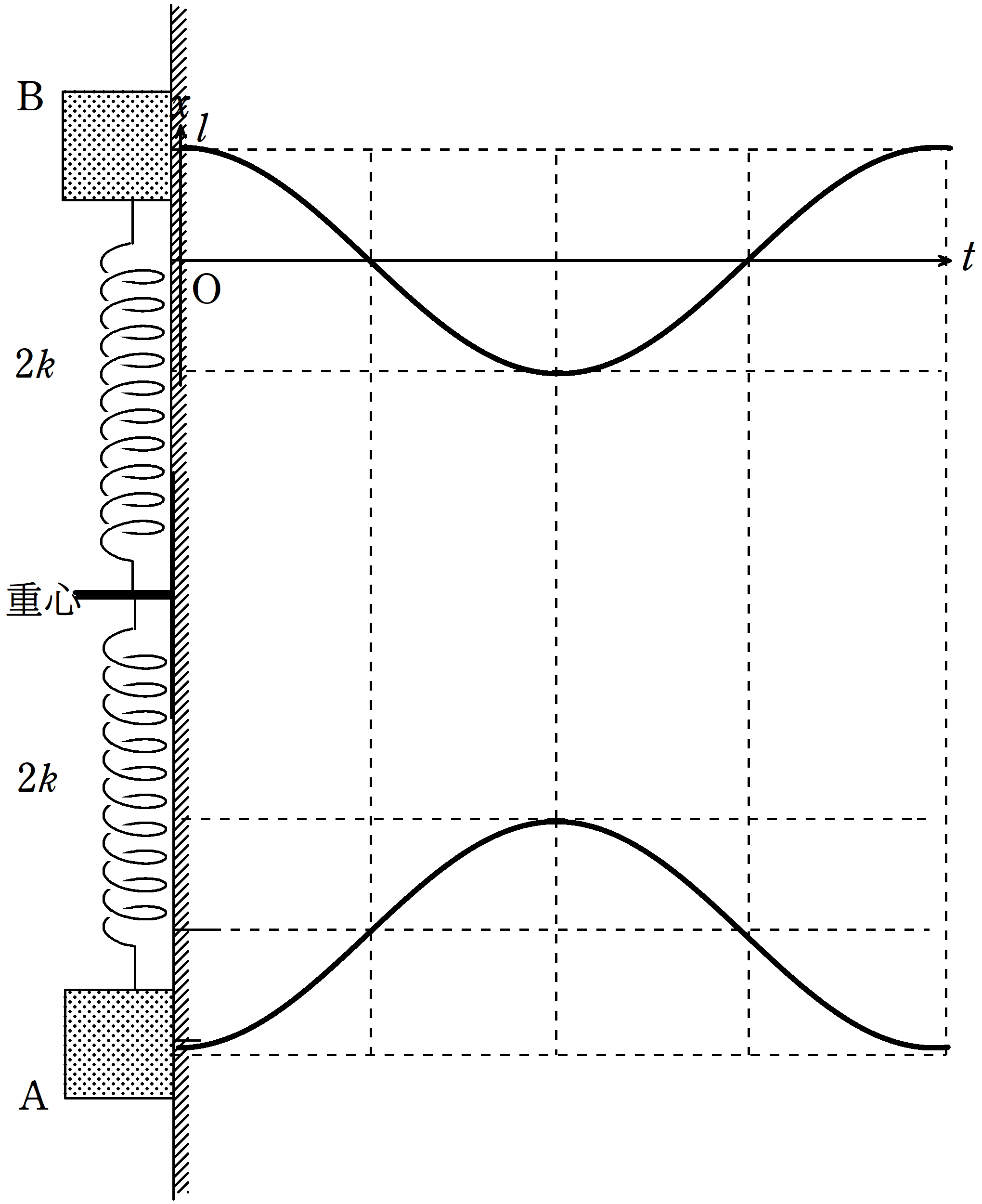
ばね定数は長さに反比例するんだったね.
理由が知りたい人は次の記事を読んでみてね.演習問題もついてるよ.
したがって,Bの方のばね定数を$k_{\rm B}$とすると
$k:k_{\rm B}=1:\dfrac{1}{\dfrac{1}{2}}=1:2$
$\therefore$ $k_{\rm B}=2k$(答)
(3)
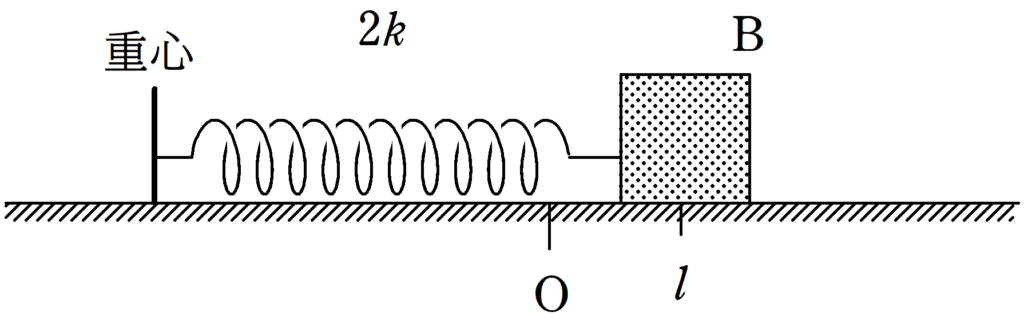

ばね全体を$2l$だけ伸ばしていて,重心はAとBの中点にあるから,重心からみたBの方のばねの伸びは$l$なんだね.
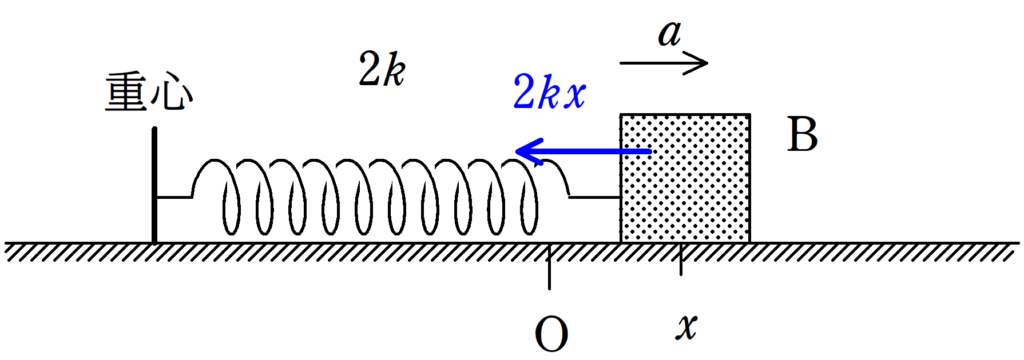

問題での設定どおり,自然長の位置を原点として,位置$x$にあるときの物体Bの加速度を$a$としましょう.
★ 重心からみた物体Bの運動方程式
$ma=-2kx$(答)

この運動方程式から,振動の中心$x_{0}$,角振動数$\omega$,周期$T$は次のようになります.
$x_{0}=0$,$\omega=\sqrt{\dfrac{2k}{m}}$,$T=2\pi\sqrt{\dfrac{m}{2k}}$
(4)

$t=0$で最大の位置にいて,負の方向へ動き出すんだから$\cos$型だね.
したがって,$x$と$t$の関係は次のようになるよ.
$x=l\cos\sqrt{\dfrac{2k}{m}}t$ (答)

ちなみに,グラフをかくと次のようになります.
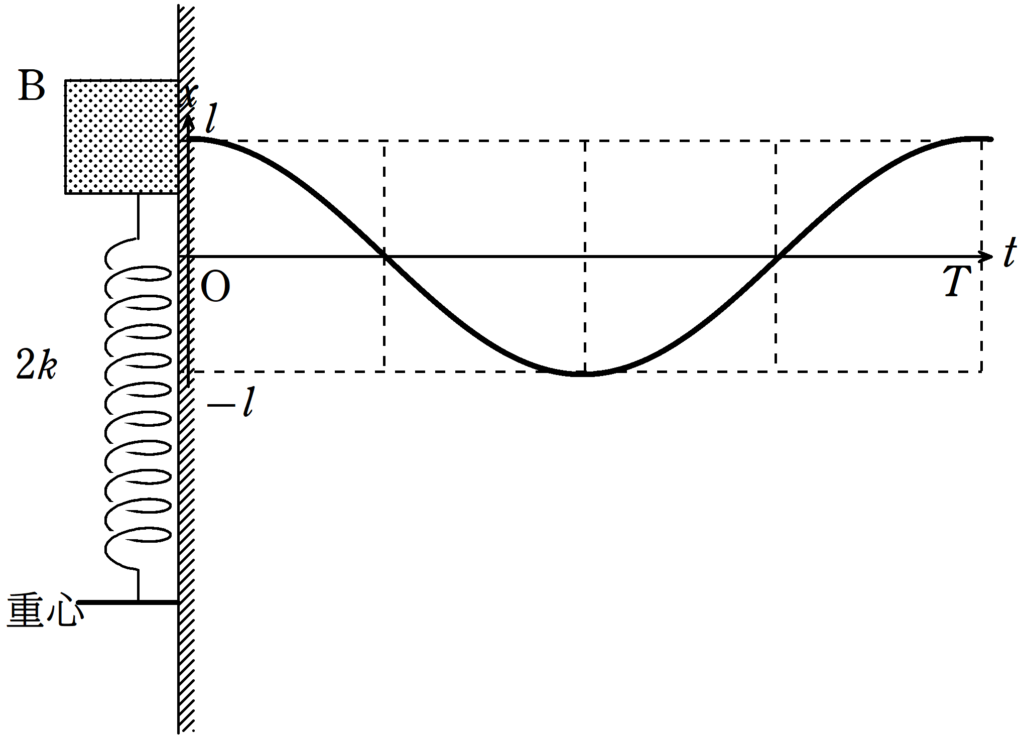

AもBとまったく同じ条件だから,同じ運動になるはずだよね.

はい.AとBを同時にかくと,次のようになります.
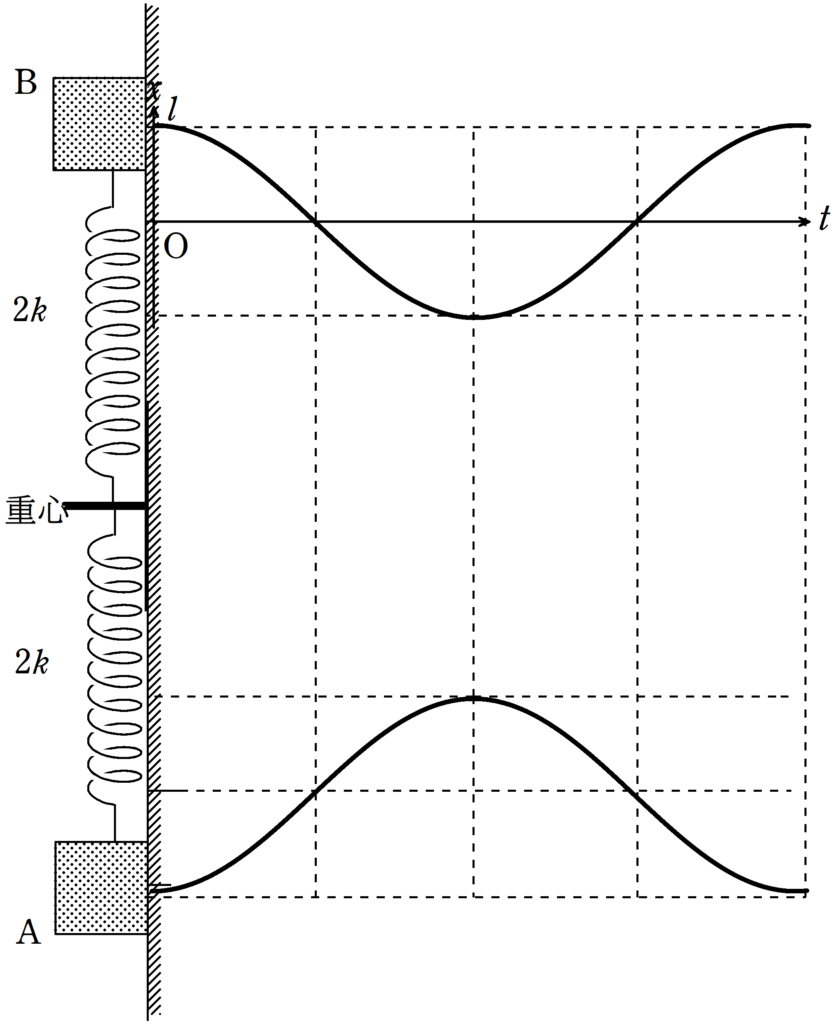

角振動数が同じだから,同じタイミングで遠ざかって,同じタイミングで近づくんだね.

コメント
[…] […]