
前回の内容はこちらです.
あらかじめ解いておくと理解しやすいかと思います.
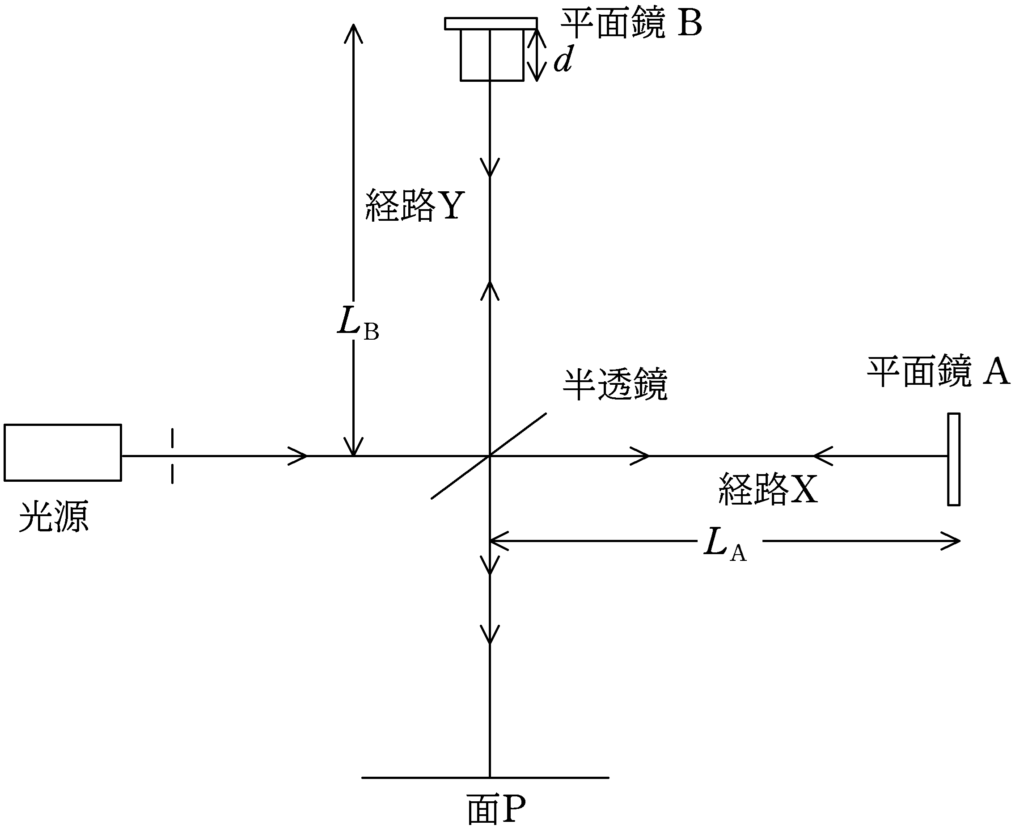
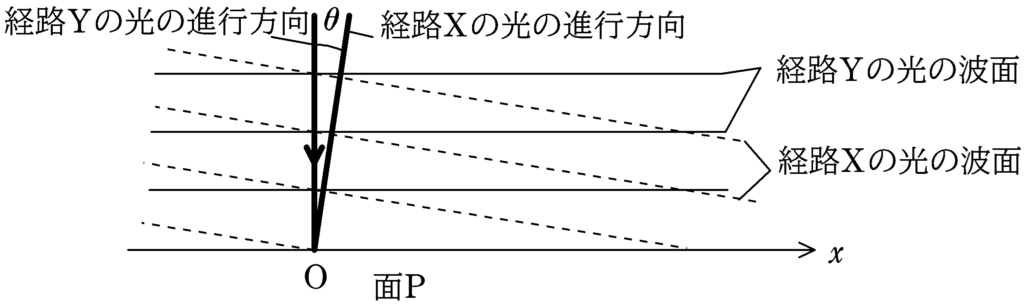
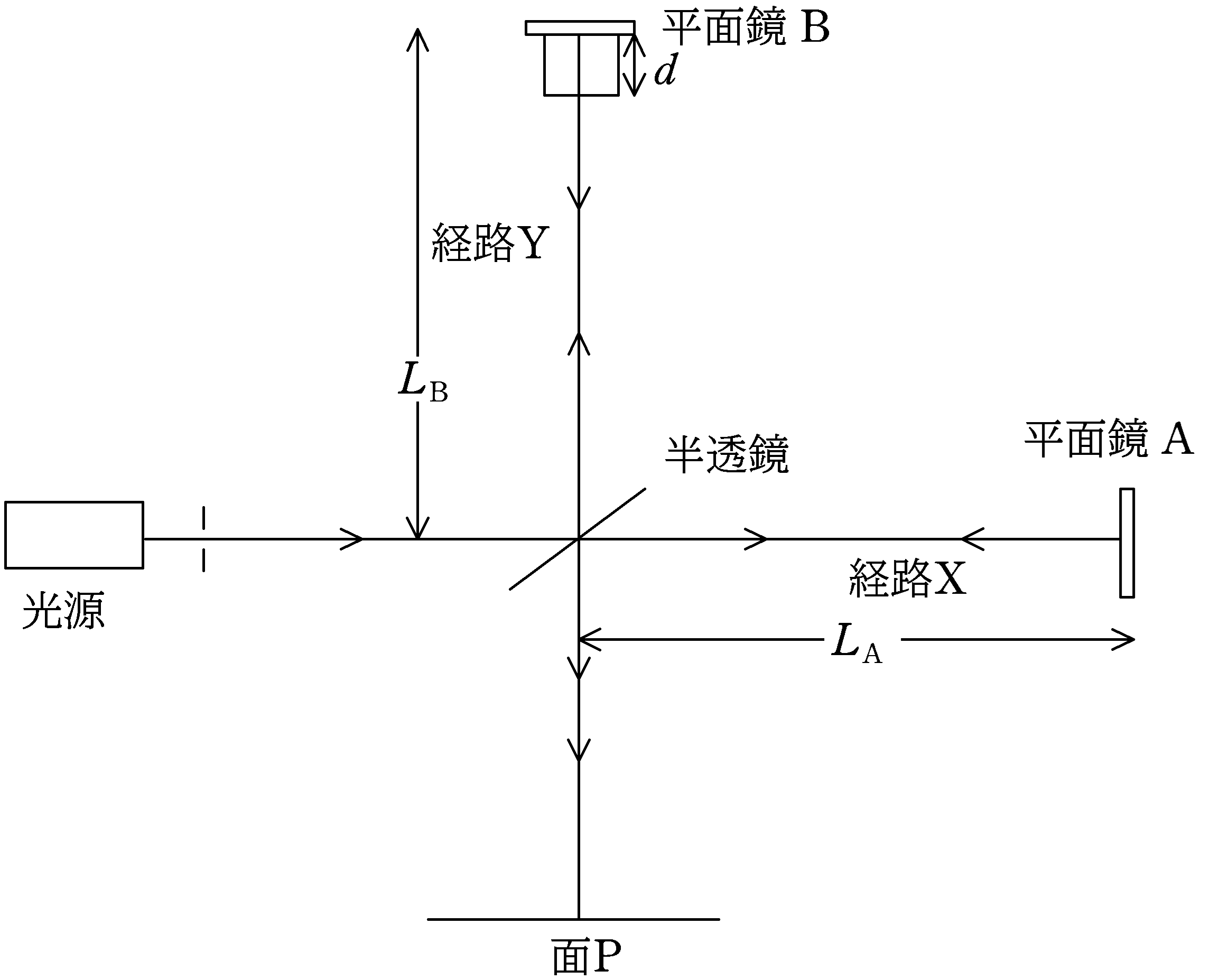
上図に示す装置で光の干渉の実験を行う.単色光源を出た波長$\lambda$の光は半透鏡で2つに分けられ,一方は平面鏡$\rm A$で反射されて,同じ経路をもどり,その一部が半透鏡を反射して面Pに到達する(経路$\rm X$).他方は平面鏡$\rm B$で反射されて同じ経路をもどり,その一部が半透鏡を透過し,面Pに到達する(経路$\rm Y$).経路$\rm Y$を通った光を面Pに垂直に入射させ(入射角$0^{\circ}$),経路Xを通った光を十分小さな入射角$\theta$で入射させた.その結果,2つの光がつくる干渉縞が面Pで観測された.2つの光は平面波であるとしてよい.下図のように,$x$軸をとるとき,次の問いに答えよ.
(1) 鏡Bの表面に厚さ$d$,屈折率$n\,(>1)$の透明薄板を装着したところ,干渉縞の間隔は変わらず,干渉縞の最も明るい部分が,透明薄板を装着する前に観測した位置とちょうど同じ位置に観測された.正の整数$m$を用いて,$d,n,\lambda$の間の関係式をかけ.
(2) (1)の透明薄板を研磨機によって薄く研磨した.研磨した後,干渉縞は$x$軸の正負どちらに移動するか.

干渉による位相差の条件をまとめると次のようになります.
地点Pにおける2つの波の位相差を$\phi$,整数を$m$とすると,
強め合いの条件:$\phi=2\pi m$
弱め合いの条件:$\phi=(2m+1)\pi $
位相差$\phi$は次の3つの要素で決まる.
$\phi_{1}$:初期位相のずれ
同位相なら$\phi_{1}=0$,逆位相なら$\phi_{1}=\pi$
$\phi_{2}$:反射による位相のずれ
自由端反射なら$\phi_{2}=0$,固定端反射なら$\phi_{2}=\pi$
$\phi_{3}$:距離の差(屈折率が変わることで生じる光学的な距離の差を含む)による位相のずれ
距離の差が$\Delta l$のとき,次の比例式を立てて,位相差$\phi_{3}$を計算する.
$2\pi : \lambda =\phi_{3} : \Delta l$
$\therefore \phi_{3}=\dfrac{2\pi}{\lambda}\Delta l$
このとき,位相差$\phi$は
$\phi=\phi_{1}+\phi_{2}+\phi_{3}$
(1)

薄板を入れる前の明線の位置と薄板を入れた後の明線の位置が同じなので,それぞれの強め合いの条件の式を立てます.
以下,半透鏡から鏡Aまでの距離を$L_{\rm A}$,半透鏡から鏡Bまでの距離を$L_{\rm B}$としましょう.
※ 実際は半透鏡での反射によって,2経路の位相差が$\pi$分ずれ,強め合いの条件と弱め合いの条件が真逆になりますが,差をとると同じ答えが出ます.
★薄板を入れる前の強め合いの条件
$l_{1}$を整数として
$\dfrac{2\pi}{\lambda}\times 2L_{\rm B}-\dfrac{2\pi}{\lambda}\times 2L_{\rm A}=2\pi\times l_{1} \cdots (\ast)$
★薄板を入れた後の強め合いの条件
$l_{2}$を整数とする.薄板内の波長は$\lambda_{1}=\dfrac{\lambda}{n}$になるので分けて計算をすることに注意
$\dfrac{2\pi}{\lambda}\times (2L_{\rm B}-2d)+\dfrac{2\pi}{\dfrac{\lambda}{n}}\times 2d-\dfrac{2\pi}{\lambda}\times L_{\rm A}=2\pi\times l_{2}$
$\therefore\,\, \dfrac{2\pi}{\lambda}\times \{2L_{\rm B}+2(n-1)d\}-\dfrac{2\pi}{\lambda}\times 2L_{\rm A}=2\pi l_{2} \cdots (2\ast)$

$n>1$なので,$(\ast)$の左辺より,$(2\ast)$の左辺の方が大きいことがわかります.つまり,それぞれの右辺を比べると,$l_{1}<l_{2}$です.そこで,$(2\ast)-(\ast)$を計算します.
★ $(2\ast)-(\ast)$
$\dfrac{\cancel{2\pi}}{\lambda}\times 2(n-1)d=\cancel{2\pi}\times (l_{2}-l_{1})$

上式で$l_{2}-l_{1}=m\,(>0)$とおきます.
$\dfrac{2(n-1)d}{\lambda}=m$ $\therefore\,\, 2(n-1)d=m\lambda$(答)
(2)
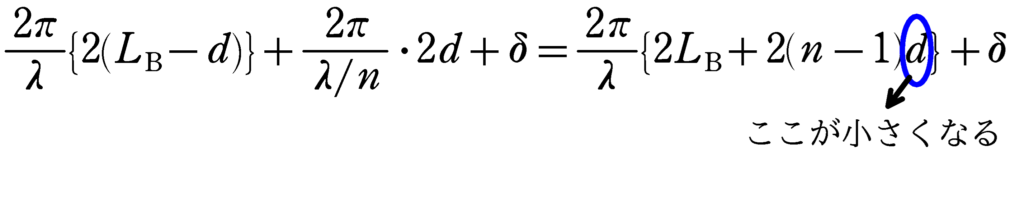

光源に対する面Pでの経路Yの波の位相の遅れは上のようになります.$\delta$は光源から半透鏡と半透鏡から面Pまでの分の位相のずれです.
薄板を研磨すると$d$が小さくなるので,上図の青い部分の$d$が小さくなります.すると,
「光源に対する経路Yの面Pでの位相のずれが小さくなる」
とも言えるし
「光源に対する経路Yの面Pまでの光学的な距離が近くなる」
とも言えるし
「光源に対する経路Yの面Pまでの波の数が少なくなる」
とも言えるし
「光源に対する経路Yの面Pまでに届く時間が短くなる」
とも言えます.
上のどれを使って考えるかは好き好きですが,一貫していえることが,研磨することで,もともとあった波面(青線横棒)より少し進んだところに波面がくる(赤細線)ようになることで,元の腹線(太黒線)が移動し赤色の腹線になります.
そうすると,下図のように腹線が右方向に移動し,明線の位置も$x$軸正方向へ移動(答)することになります.
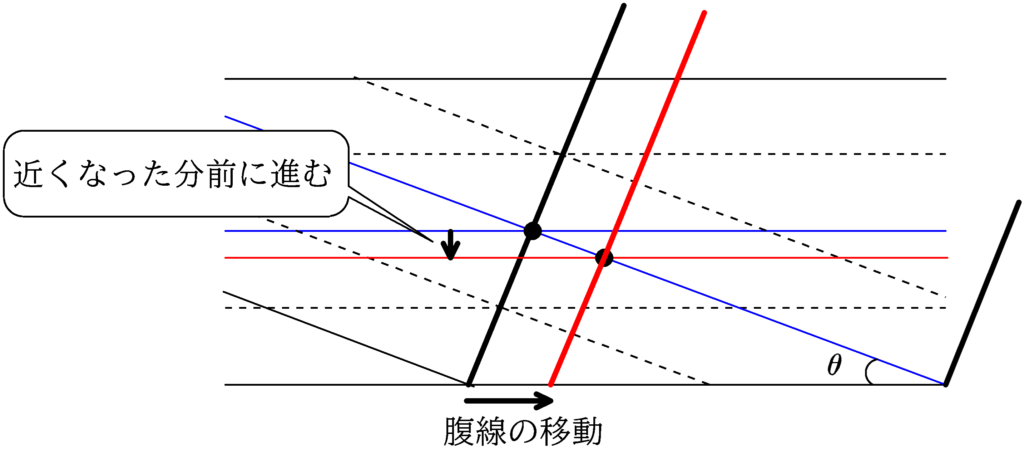

光学的な距離が近くなった分,波面を前に移動させて,その交点をみて新たな明線を見つけるようにするとよいでしょう.




コメント