
今回は,凸レンズのレンズの式の導出です.
レンズの式は余裕があったら覚えてもよいですが,自分で導出できた方が応用もきくでしょう.
作図と相似がわかれば,そこまで難しくないので,ぜひ挑戦してみてください.
前回の内容なこちらです.
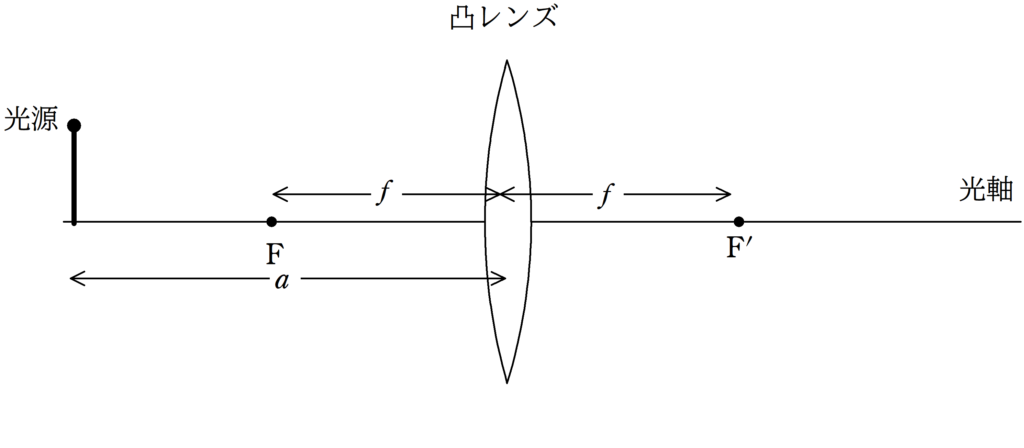
上図のような焦点が$\rm F$,$\rm F^{\prime}$である焦点距離$f$の凸レンズがある.
凸レンズより,距離$a(a>f)$だけ離れた位置に,光軸に垂直な光源が立てられている.
光源から出た光は凸レンズを通過後,実像をつくる.
凸レンズと実像との距離を$b$とするとき,$a , b , f$の関係式を求めよ.
<解答>

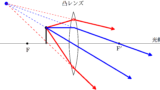
まずは,作図からしてみよう.
次の3つの代表光線を利用して光線の作図ができるんだったね.
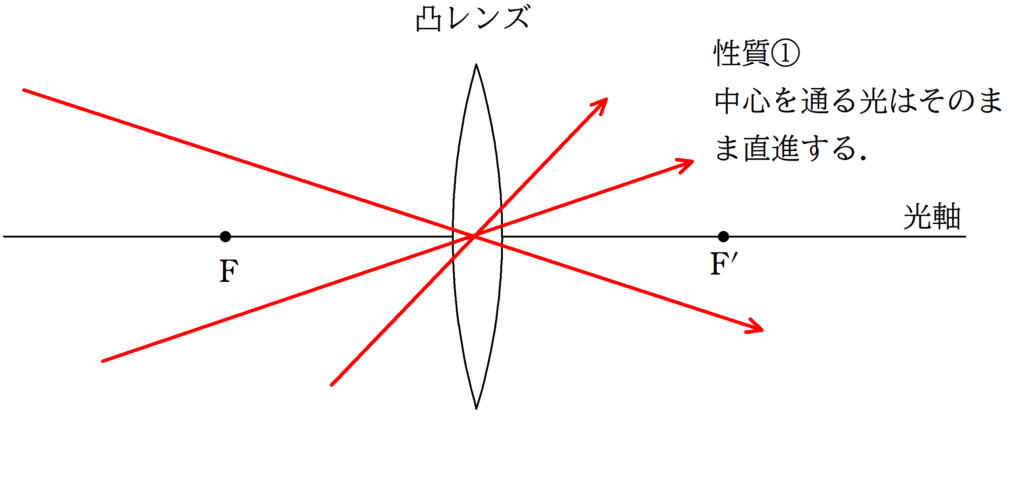
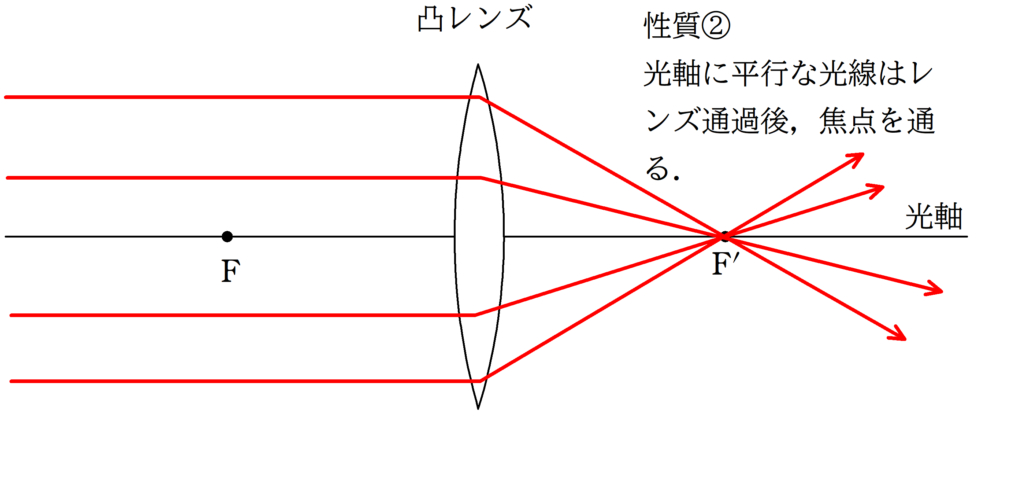
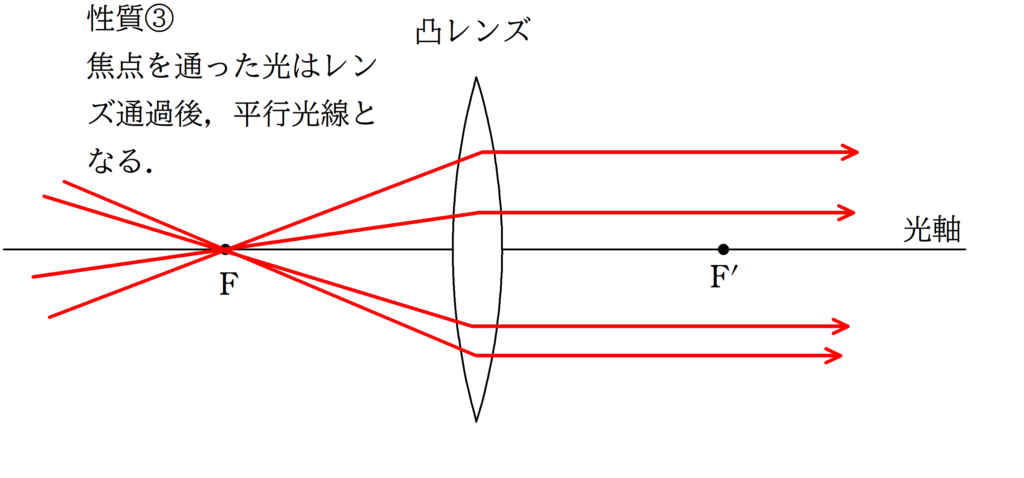

光軸に平行な光線と,中心を通る光線によって,光が集まる場所が予想できるね.
この光が集まったところに実像ができるよ.
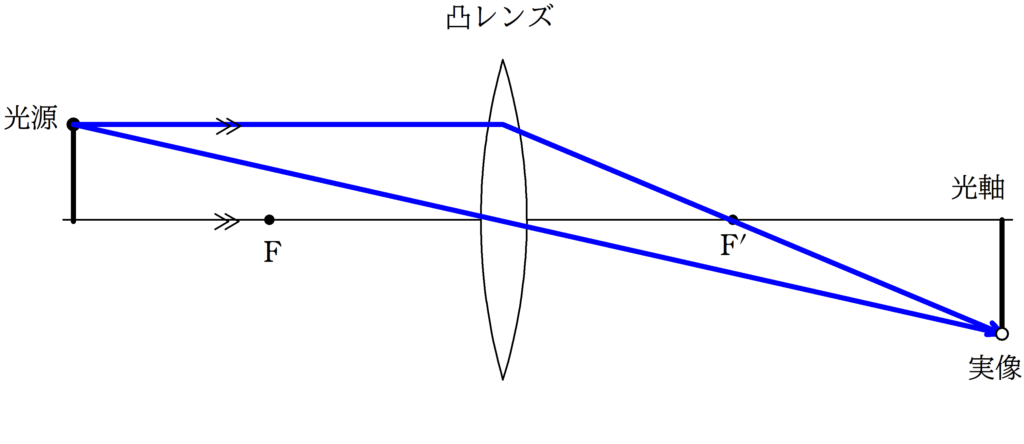

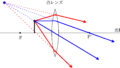
そうしたら,次は2組の相似な直角三角形を見つけるよ.
ここで,光源の高さを$X$,実像の高さを$Y$としよう.
$X$や$Y$を絡めた相似な直角三角形を探してください.
すると,下の2組が見つかるはずです.
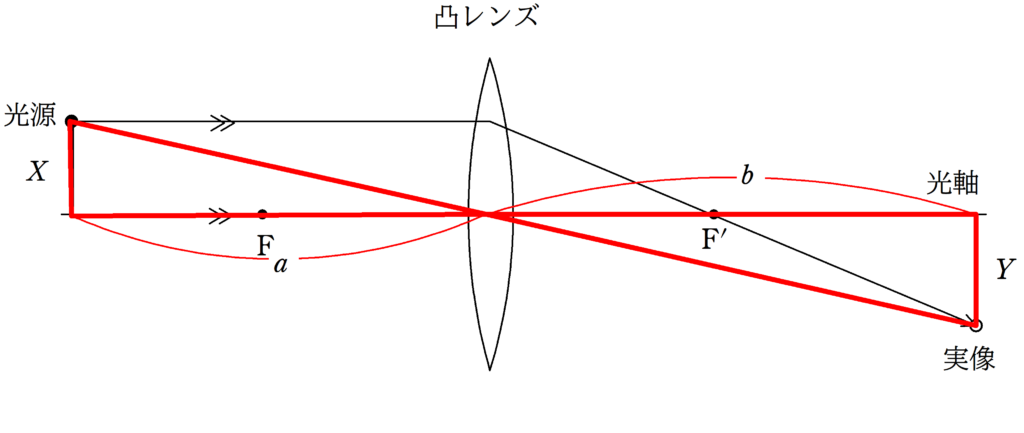
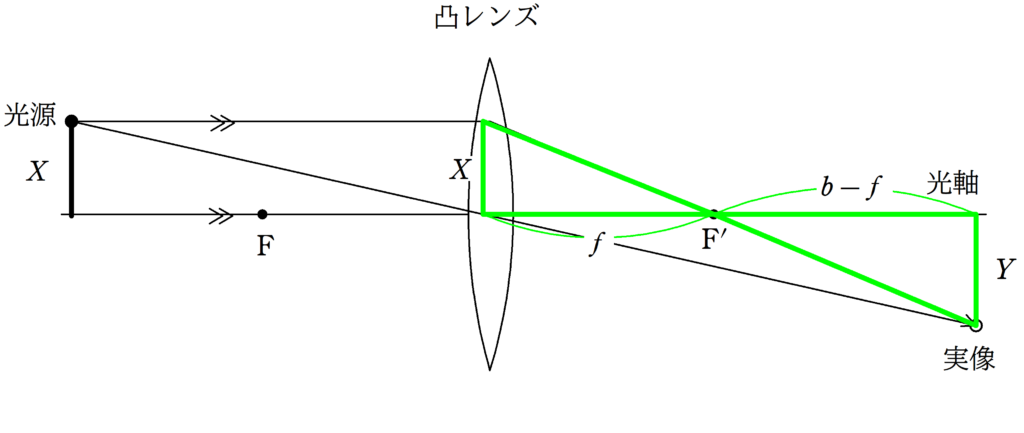

赤い方の相似な図形の相似比と,緑の方の相似な図形の相似比を書き出してみよう.
$\dfrac{Y}{X}=\dfrac{b}{a}$ $\dots (\ast)$
$\dfrac{Y}{X}=\dfrac{b-f}{f}$ $\dots (2\ast)$
$(\ast)$,$(2\ast)$の左辺が同じなので
$\eqalign{\dfrac{b}{a}&=\dfrac{b-f}{f}\cr bf&=ab-af \cr bf+af&=ab}$
両辺$abf$で割ると
$\dfrac{\cancel{bf}}{a\cancel{bf}}+\dfrac{\cancel{af}}{\cancel{a}b\cancel{f}}=\dfrac{\cancel{ab}}{\cancel{ab}f}$
$\therefore \dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}f$
答え $\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}f$

では,もう1題解いてみましょう.
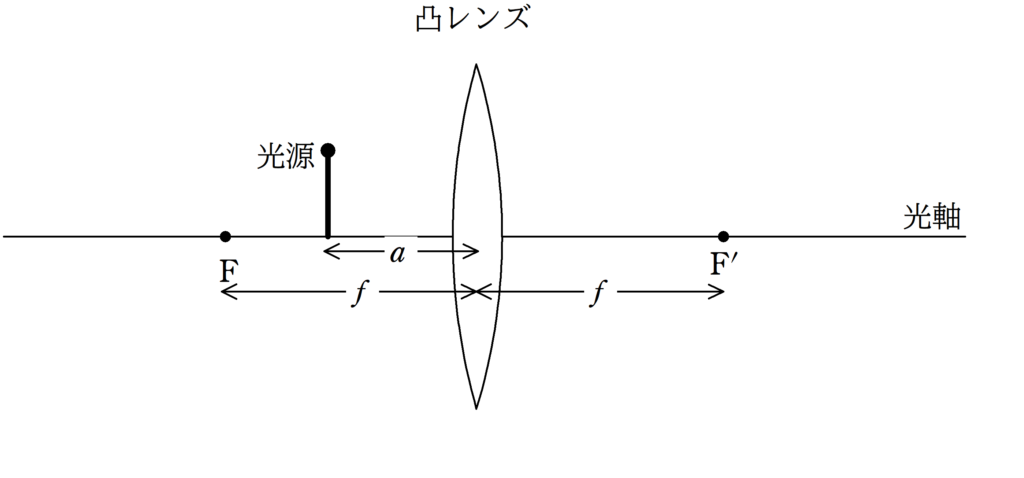
上図のような焦点が$\rm F$,$\rm F^{\prime}$である焦点距離$f$の凸レンズがある.
凸レンズより,距離$a(a<f)$だけ離れた位置に,光軸に垂直な光源が立てられている.
光源から出た光は凸レンズを通過後,発散し,レンズ前方に虚像ができる.
凸レンズと虚像との距離を$b$とするとき,$a , b , f$の関係式を求めよ.
<解答>

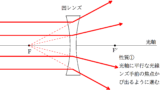
まずは,作図をしてみよう.
今回は,平行光線と中心を通る線が交わらないので,反対側に線を伸ばすといいんだったね.
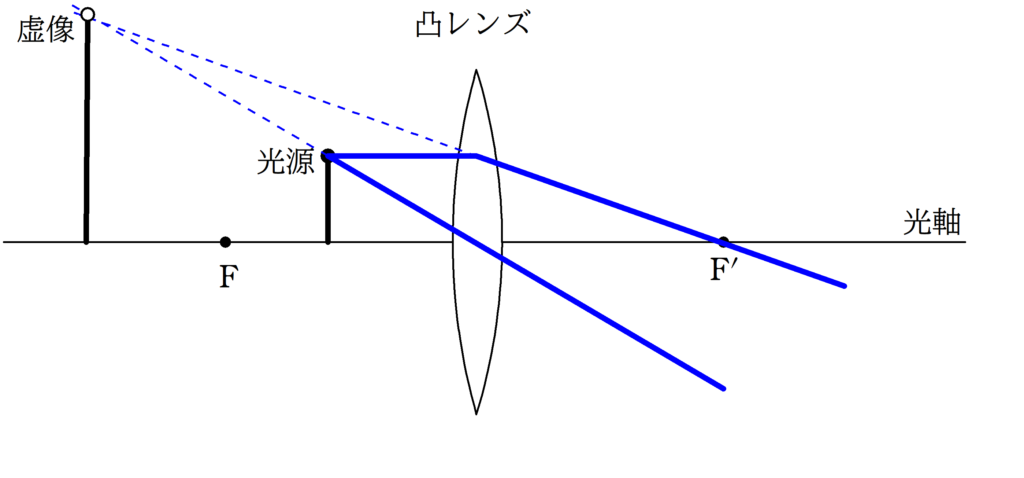

平行光線や中心を通る線だけではなく,光源から出たあらゆる光線はこの虚像から出てきたように見えます.
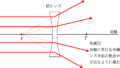
それでは,光源の高さを$X$,虚像の高さを$Y$として,2組の相似な図形を見つけてみましょう.
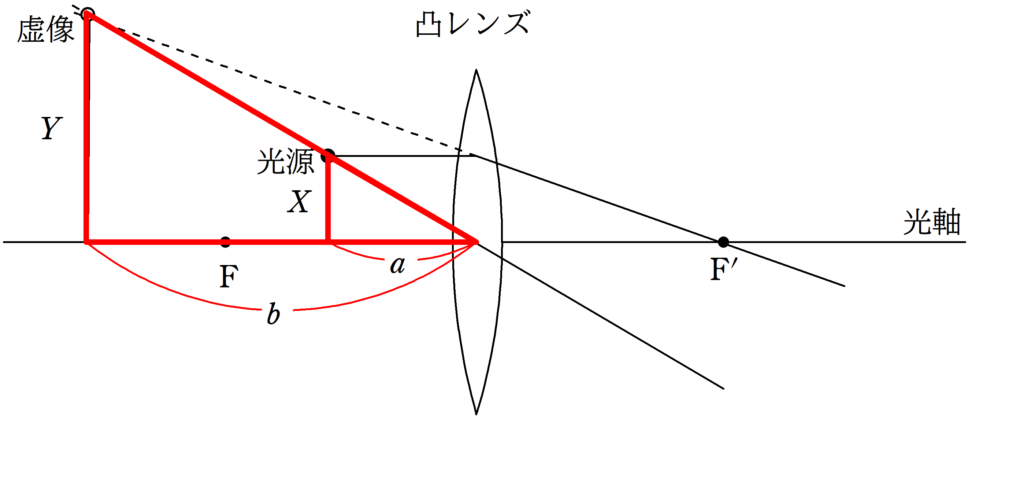
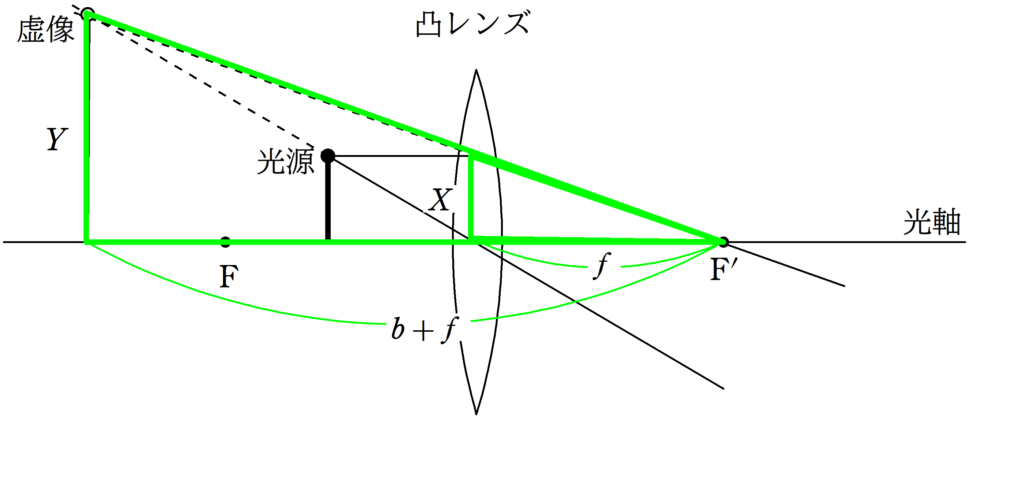

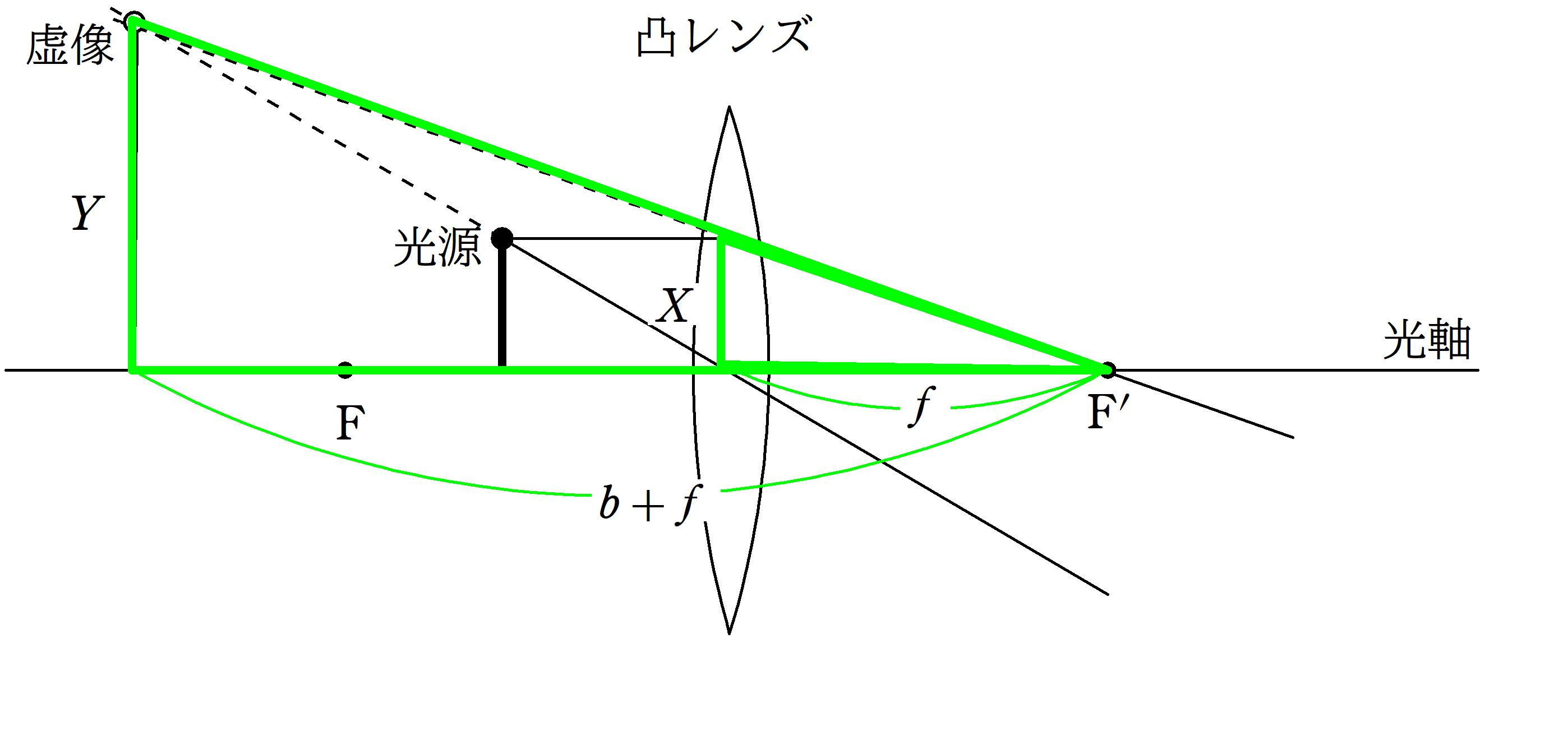
やはり,赤い方の相似比と緑の方の相似比を考えてみます.
$\dfrac{Y}{X}=\dfrac{b}{a}$ $\dots (3\ast)$
$\dfrac{Y}{X}=\dfrac{b+f}{f}$ $\dots (4\ast)$
$(3\ast)$,$(4\ast)$より
$\eqalign{\dfrac{b}{a}&=\dfrac{b+f}{f}\cr bf&=ab+af \cr bf-af&=ab}$
両辺$abf$で割って
$\dfrac{1}{a}-\dfrac{1}{b}=\dfrac{1}{f}$ (答え)

最後にまとめておきましょう.
焦点距離$f$の凸レンズと光源の距離を$a$,凸レンズと像までの距離を$b$とする.
★ 実像ができるとき
$\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{f}$
★ 虚像ができるとき
$\dfrac{1}{a}-\dfrac{1}{b}=\dfrac{1}{f}$

次回の内容はこちらです.

コメント
[…] […]
[…] レンズの演習問題① 凸レンズの作図① レンズの演習問題③ レンズの式(凸レンズ) […]