
今回は中心がずれたときの$x$の式の表現を練習しよう!
前回の記事はこちら
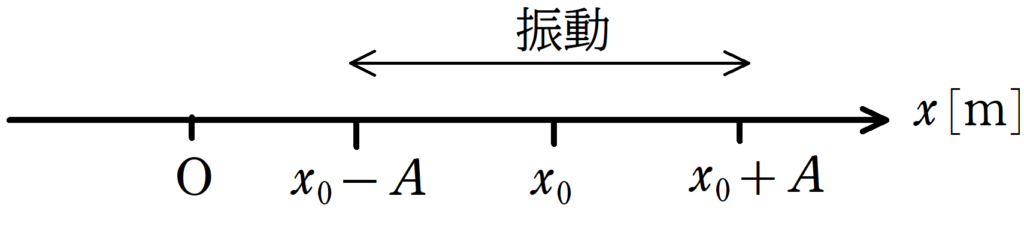
ある物体が,$x=x_{0}[\rm{m}]$を中心に$x$軸上を振幅が$A[\rm{m}]$,角振動数$\omega [\rm{rad/s}]$,で単振動している.次の運動について,時刻$t[\rm{s}]$における位置$x[\rm{m}]$の式を答えよ.
(1) $t=0 \rm{s}$に$x=x_{0}[\rm{m}]$を出発して$x$軸の正の方向へ出発する運動.
(2) $t=0 \rm{s}$に$x=x_{0}-A[\rm{m}]$を出発して$x$軸の正の方向へ出発する運動.
(3) $t=0 \rm{s}$に$x=x_{0}+A[\rm{m}]$を出発して$x$軸の負の方向へ出発する運動.
(4) $t=0 \rm{s}$に$x=x_{0}[\rm{m}]$を出発して$x$軸の負の方向へ出発する運動.
<解答>
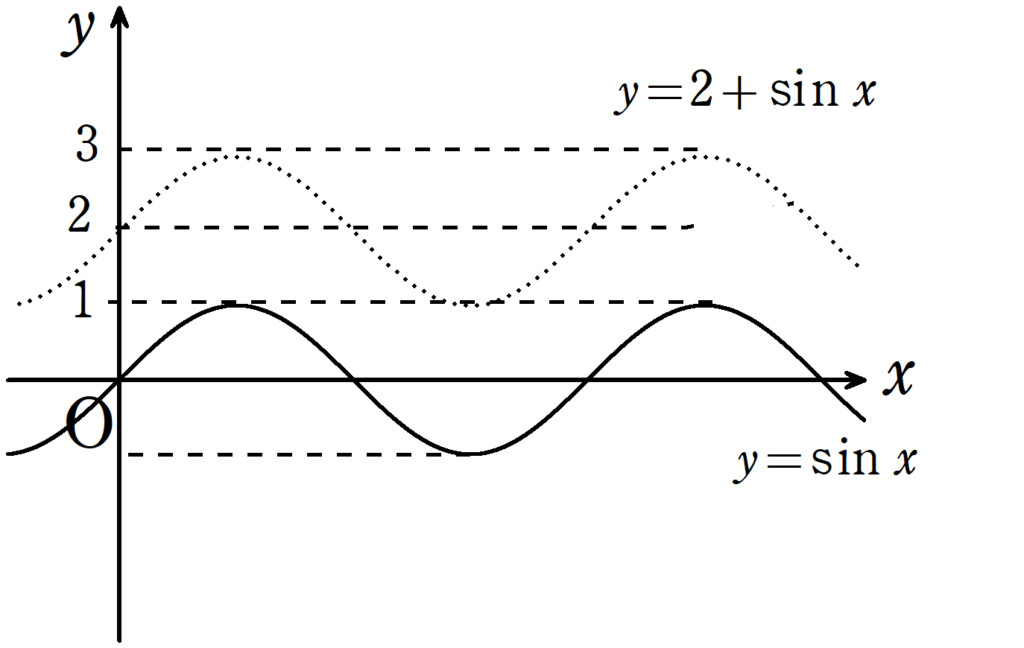
たとえば,$y=2+\sin x$は$y=\sin x$のグラフを$y$軸方向へ$+2$平行移動したものです.
単振動の問題では,中心が原点にあるとは限りません.
一般的は位置$x$の式は次のようになります.
$x=振動の中心+振動部分$
振動部分に入るのは$\sin$や$\cos$です.
(1) 振動の中心が$x_{0}$で,中心からスタートし,正の方向へ移動するので,$\sin$型.したがって,$x=x_{0}+A\sin (\omega t)[\rm{m}]$
(2) 振動の中心が$x_{0}$で,最小の位置からからスタートし,正の方向へ移動するので,$-\cos$型.したがって,$x=x_{0}-A\cos (\omega t)[\rm{m}]$
(3) 振動の中心が$x_{0}$で,の最大の位置からからスタートし,負の方向へ移動するので,$\cos$型.したがって,$x=x_{0}+A\cos (\omega t)[\rm{m}]$
(4) 振動の中心が$x_{0}$で,中心からスタートし,負の方向へ移動するので,$-\sin$型.したがって,$x=x_{0}-A\sin (\omega t)[\rm{m}]$

2回に渡って,$x$の式を立てる練習をしました.それでは,
- 振動の中心
- 初期位相
- 振幅
- 角振動数,周期
はどのように調べるのでしょうか?
次回からは具体的に$x$の式を求めるにあたって必要な4つの要素の調べ方についての演習を行います.
次回の問題はこちら




コメント
[…] [基本]単振動の演習問題② の続きです.今回は振動の中心を求める練習です.振動の中心は運動方程式から判断できます.質量$m$,加速度$a$,正の比例定数を$k$,物体の座標を$x$,中心座標を$x_{0}$とするとき,単振動の運動方程式は […]
[…] 次の問題はこちら […]
[…] […]