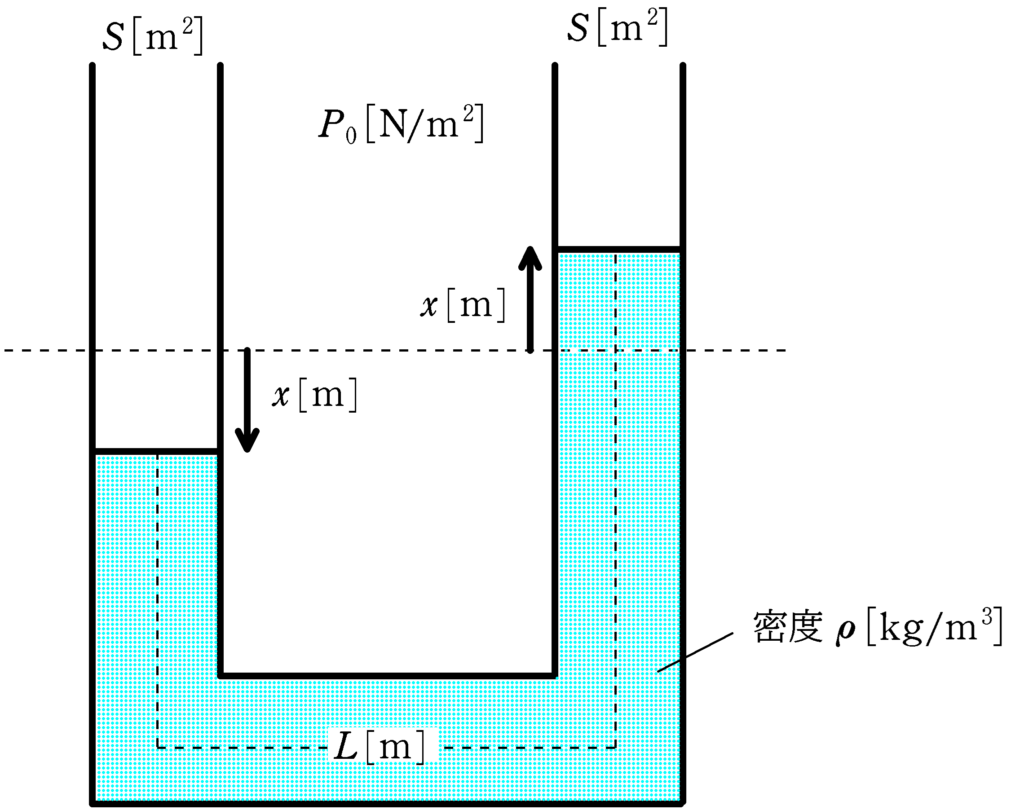
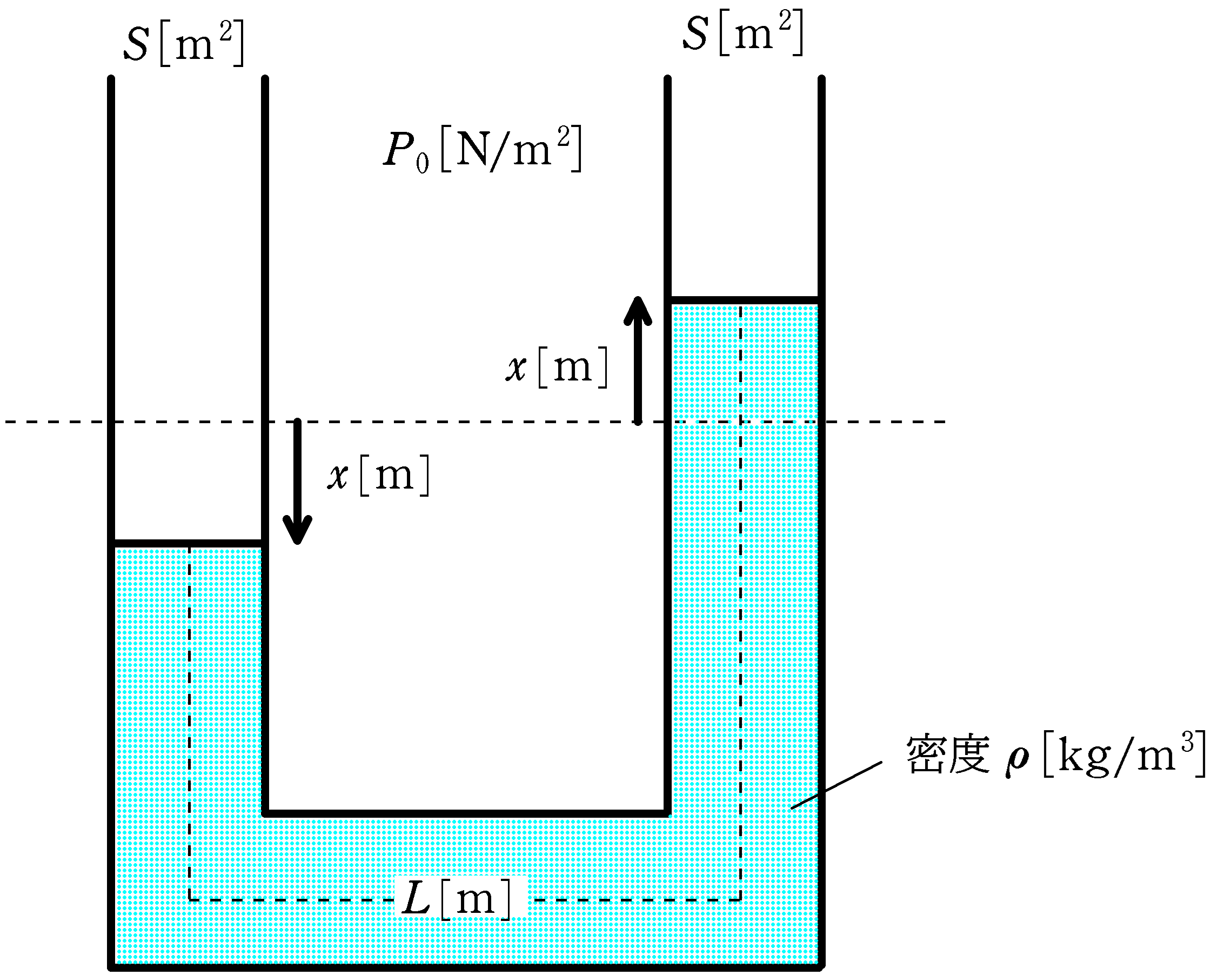
断面積$S\, [\rm m^{2}]$のU字管に密度$\rho\, [\rm kg/m^{3}]$の液体が入っている.この液体の体積は$SL\, [\rm m^{3}]$である.U字管の左右の液面に高さの差をつけて開放したところ,液面は単振動をした.ただし,大気圧は一定の$P_{0}\, [\rm N/m^{2}]$であり,重力角度加速度の大きさを$g\, [\rm m/s^{2}]$とする.
このとき,液面の単振動の周期$T\, [\rm s]$を求めよ.
<解答>

これって,液体には,重力と大気が押す力しかはたらいていないよね??
大気が押す力は右側の液面も左側の液面も$P_{0}S\, [\rm N]$だから,復元力0なんじゃないの??本当に単振動なんて起こるのかな??

確かに,今回は大気が押す力は同じなので,この力は復元力にはなりません.
しかし,右側と左側の液体で体積が異なるので,重さも異なります.
この重さの差が復元力となるんです.
なにも力を加えないと左右の液面は同じ高さになります.このときの右側の液面を原点として,右側の液面が$x\, [\rm m]$だけ上に変位したときのことを考えましょう.このときの鉛直上向きの加速度を$a\, [\rm m/s^{2}]$とします.
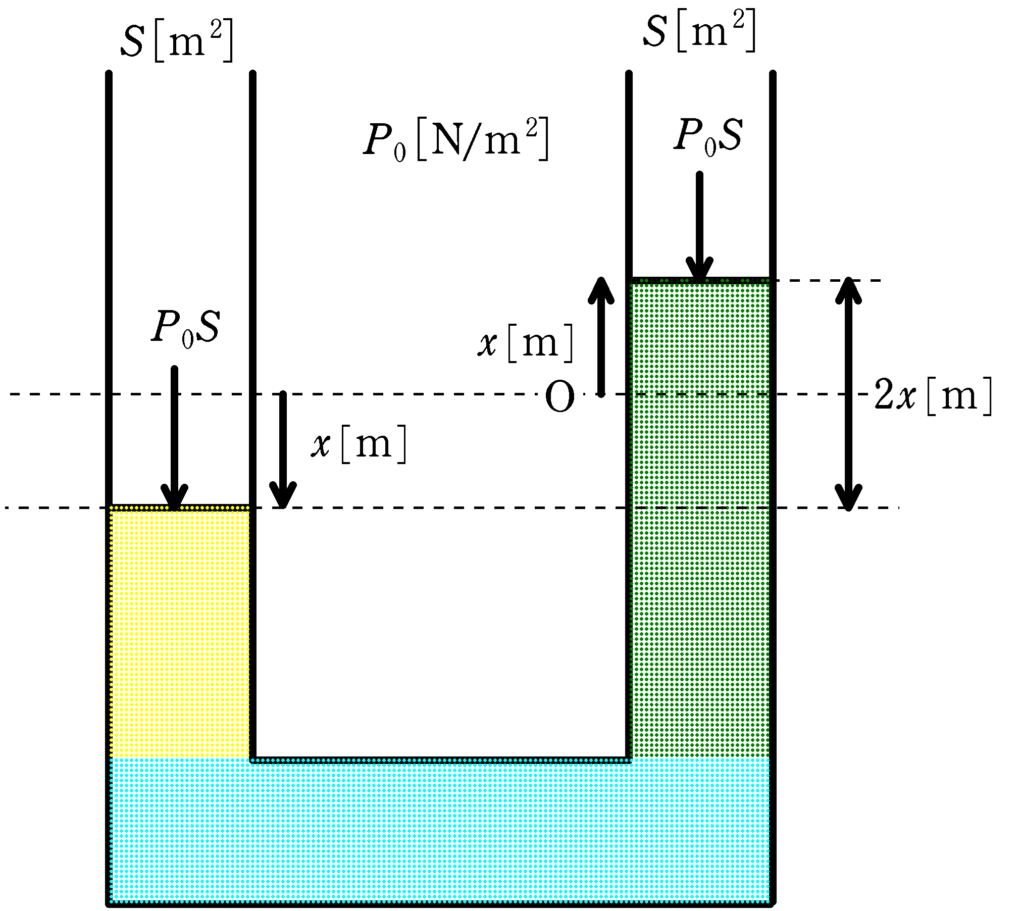

なるほど!確かに,左側の液体と右側の液体では重さが違うね.右側の液体は左側の液体より,$2x\, [\rm m]$分長いから,$\rho \cdot 2x\cdot Sg$だけ重いんだ.
つまり,液体には,原点にもどるように重さ$2\rho Sxg$の力がはたらくんだね.
★ 運動方程式
$\rho SL a=-2\rho Sg x$
質量を$m$,加速度を$a$,物体の座標を$x$,$x_{0}$を定数,$k$を正の定数とする.
運動方程式が以下で表されている.
$ma=-k(x-x_{0})$
このとき,振動の中心は$x_{0}$,角振動数$\omega$と周期$T$は次のようになる.
$\omega=\sqrt{\dfrac{k}{m}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{m}{k}}$

運動方程式より,角振動数$\omega$と,周期$T$は次のようになるね.
$\omega=\sqrt{\dfrac{2\rho Sg}{\rho SL}}=\sqrt{\dfrac{2g}{L}}$
$T=\dfrac{2\pi}{\omega}=2\pi\sqrt{\dfrac{L}{2g}}$ (答)


コメント