[基本]円運動演習1　円錐振り子

問題

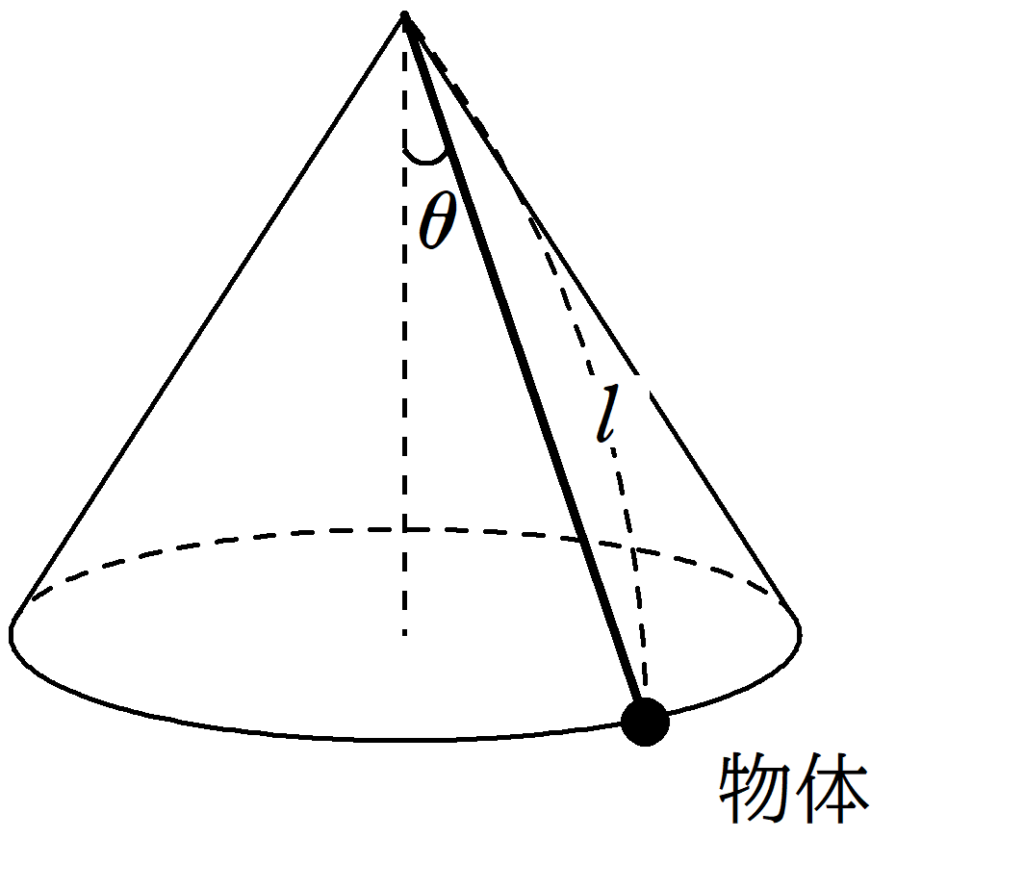
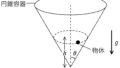
図のように，長さ$l$の軽くて伸びない糸の一端を固定し，他端に質量$m$の物体をとりつけ，速さ$v$で円錐振り子運動させる．物体が運動する平面は水平面に平行であり，物体は鉛直線から角度$\theta$を保ちながら円運動している．重力加速度の大きさを$g$として，次の問いに答えよ．

(1)　物体にはたらく張力の大きさを$S$とする．物体の向心方向の運動方程式と，鉛直方向のつり合いの式をそれぞれ立てよ．

(2)　円運動の周期$T$を，$g$，$l$，$\theta$を用いて表せ．

＜解答＞

(1)

NEKO

等速円運動の問題で立てて欲しいのは次の2式です．

NEKO

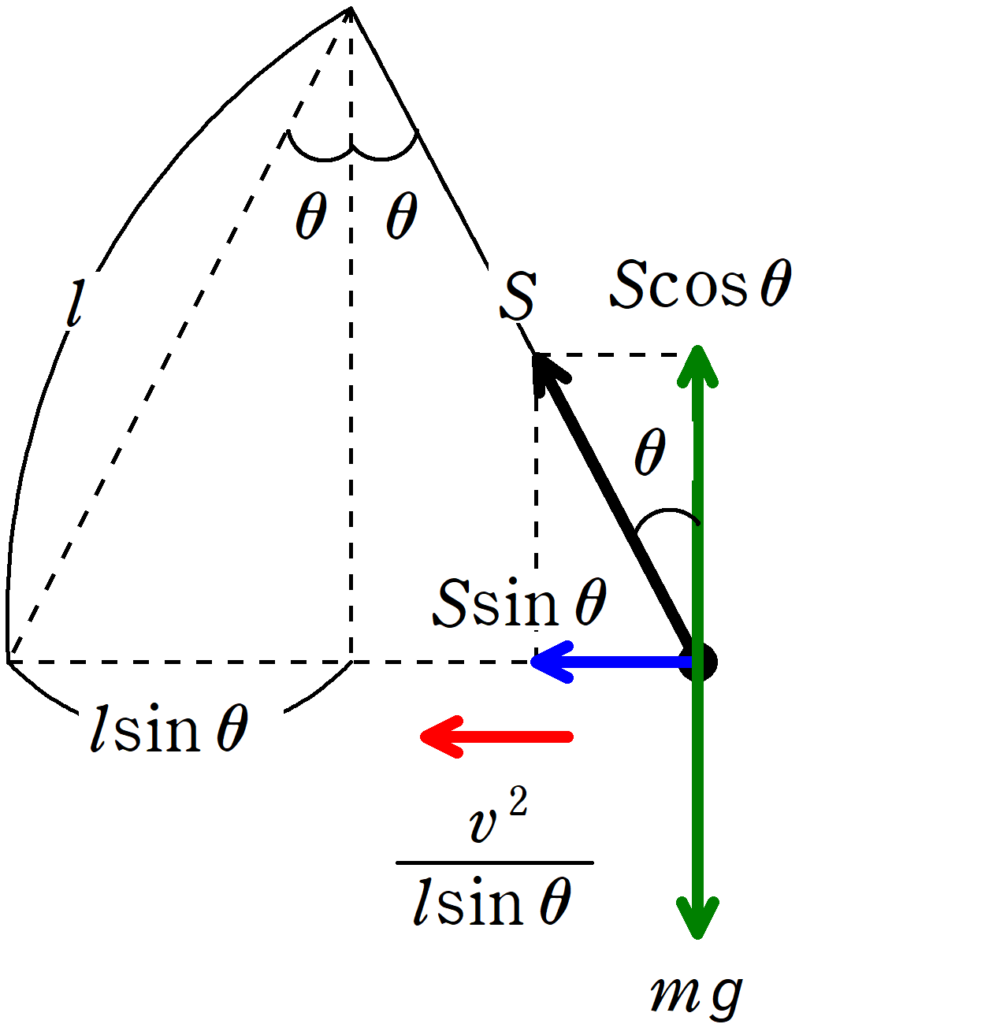
張力の大きさを$S$としたとき向心力の大きさは$S\sin\theta$です．

そして，円運動の半径は$l\sin\theta$です．（$l$じゃないよ）

すると，向心方向の加速度は$\dfrac{v^{2}}{l\sin\theta}$です．

向心方向の運動方程式と鉛直方向のつり合いの式を立てましょう．

★　向心方向の運動方程式

$m\dfrac{v^{2}}{l\sin\theta}=S\sin\theta$　(答) $\dots　(\ast)$　

★　鉛直方向のつり合いの式

$S\cos\theta=mg$　(答) $\dots　(2\ast)$

(2)　$(2\ast)$より，

$\therefore　S=\dfrac{mg}{\cos\theta}$　$\dots　(3\ast)$

$(3\ast)$を$(\ast)$に代入して

$m\dfrac{v^{2}}{l\sin\theta}=\dfrac{mg}{\cos\theta}\cdot \sin\theta$

$\therefore　v=\sin\theta\sqrt{\dfrac{gl}{\cos\theta}}$　$(4\ast)$

さらに，周期の式より

$\eqalign{T&=\dfrac{2\pi l\sin\theta}{v}\\&=\dfrac{1}{\sin\theta}\sqrt{\dfrac{\cos\theta}{gl}}\cdot 2\pi l\sin\theta\\&=2\pi\sqrt{\dfrac{l\cos\theta}{g}}}$　(答)